- #1
Happiness
- 679
- 30
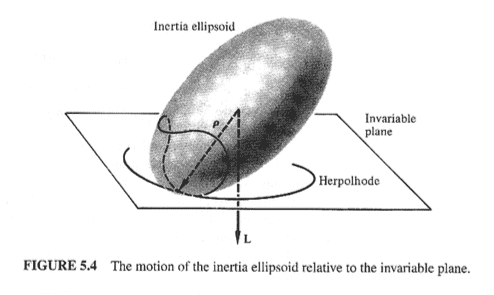
From the last few sentences of the below attached paragraph, when the inertia ellipsoid is prolate, the body cone rolls outside the space cone; when it is oblate, the body cone rolls inside the space cone.
Whether the body cone rolls outside or inside the space cone should depend on whether the body cone is rotating clockwise or anti-clockwise. Why should it depend on whether the ellipsoid is prolate or oblate?
The same sentences wrote that the ellipsoid is prolate when the (principal) moment of inertial about the symmetry axis is less than that about the other two principal axes. I believe it should be more than, rather than less than.
Suppose the symmetry axis is along the ##x_1## axis, then the principal moment of inertial about the symmetry axis is ##I_1##, according to (5.35) and (5.33). And from Fig 5.4, the semi-principal axis along ##x_1##, the symmetry axis, is longer than those along ##x_2## and ##x_3##. Thus ##I_1## should be more than ##I_2## and ##I_3##. Isn't it?


Whether the body cone rolls outside or inside the space cone should depend on whether the body cone is rotating clockwise or anti-clockwise. Why should it depend on whether the ellipsoid is prolate or oblate?
The same sentences wrote that the ellipsoid is prolate when the (principal) moment of inertial about the symmetry axis is less than that about the other two principal axes. I believe it should be more than, rather than less than.
Suppose the symmetry axis is along the ##x_1## axis, then the principal moment of inertial about the symmetry axis is ##I_1##, according to (5.35) and (5.33). And from Fig 5.4, the semi-principal axis along ##x_1##, the symmetry axis, is longer than those along ##x_2## and ##x_3##. Thus ##I_1## should be more than ##I_2## and ##I_3##. Isn't it?