PcumP_Ravenclaw
- 105
- 4
Dear all,

please see the page above, (Alan F, Beardon, Abstract Algebra and Geometry). On the page, Theorem 3.5.2 says that the set of Complex numbers from ## z^n = 1 ##, where ## |z| = 1 ## forms a group w.r.t multiplication. I want to know if...
The inverse of all elements are their complex conjugates?
inverse of the identity, z = 1∠0 is its own inverse??
is an inverse missing when n is even??
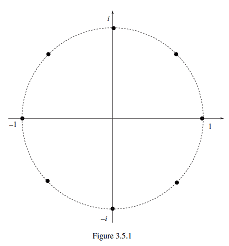
In the above diagram, n = 8. z = 1 is the inverse of itself. the three complex points above the real axis have inverses as the three complex points below the real axis. What about z = -1?? where is its inverse?? is it z = 1? why?
please see the page above, (Alan F, Beardon, Abstract Algebra and Geometry). On the page, Theorem 3.5.2 says that the set of Complex numbers from ## z^n = 1 ##, where ## |z| = 1 ## forms a group w.r.t multiplication. I want to know if...
The inverse of all elements are their complex conjugates?
inverse of the identity, z = 1∠0 is its own inverse??
is an inverse missing when n is even??
In the above diagram, n = 8. z = 1 is the inverse of itself. the three complex points above the real axis have inverses as the three complex points below the real axis. What about z = -1?? where is its inverse?? is it z = 1? why?