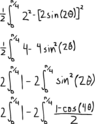Rose Petal - Circle - Area problem - Can someone check my work please?

[Pindrought]

I'd love it if someone could verify whether or not I did this problem correctly.

A stained-glass window is a disc of radius 2 (graph r=2) with a rose inside (graph of r=2sin(2theta) ). The rose is red glass, and the rest is blue glass. Find the total area of the blue glass.

So I set 2=2sin(2theta) to find where they intersect and found that at theta = pi/4 there is an intersection, so I set my bounds to be from 0 to pi/4 to find an eighth section of the total area of the blue glass.

My integral looks like so
View attachment 2174

View attachment 2175

Did I do this right?

Thanks a lot for taking the time to read

 

[MarkFL]

Looks good to me, and you have the correct result. :D

 

[soroban]

Hello, Pindrought!

Your work is correct . . . Good job!I used a simpler approach.

The area of the circle is: $$\pi(2^2) \,=\,4\pi$$.
The area of the rose is: .$$8 \times \tfrac{1}{2}\int^{\frac{\pi}{4}}_0(2\sin2\theta)^2\,d\theta$$

And subtract the two areas.