Rotating reel with load driven by a motor

[bassguitar]

Homework Statement

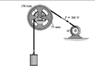
If the motor M exerts a constant force of P = 300 N on the cable wrapped around the reels outer rim, determine the velocity of the 50 kg cylinder after it has traveled a distance 2 m. Initially the system is at rest. The reel has mass 25 kg, and the radius of gyration about its center of mass A is k_a = 125 mm.

Homework Equations

I_a = m_a*k²_a
I_a*α = ΣM

The Attempt at a Solution

I_a = m_a*k²_a = 25*0.125² = 0.390625 kgm²
I_a*α = ΣM = -P*r_o + mgr_i = -300*0.15 + 50*9.81*0.075 = -8.2125kgm
α = -8.2125 / 0.390625 = -21.024rad/s²
a = α*r_i = -1.5768m/s²
s = (at²)/2 and v = at and we get that v = 2.51m/s, but the answer given is 1.91m/s.

What am I doing wrong? In the solution they use energy method which I understand, but I should be able to solve it correctly that way as well. Why do I get a different answer?

 

[Physiona]

I think firstly you'd focus on the Kinetic Energy and the work. As the reel rotates a fixed axis vC = vr rC or vr = vC rC = vC/0.075 = 13.33vC. The mass moment of inertia of the reel about its mass centers is I_a = M_rk_A², which would equal 25(0.125)² = 0.390625 kg ⋅ m₂. Thus the kinetic energy of the system is T = T_r + T_c which = ½ I_A ω_r² + m_c x v_c², which would then proceed to = ½(0.390625)(13.33v_C)² + ½(50)v_C² which would equal 59.72v_C²

There is more But I don't know how to insert the picture on here to show you, because you use that to get the answer of 1.91m/s.

 

[bassguitar]

Hi Physiona,

Thank you for the reply. I understand how to solve the problem using the energy method. What I don't get is why my attempt at a solution is wrong.

 

[haruspex]

Hi Physiona,

Thank you for the reply. I understand how to solve the problem using the energy method. What I don't get is why my attempt at a solution is wrong.

Your mgr_i term does not allow for the acceleration of the mass. A more systematic approach is to introduce a variable for the tension in the vertical cable and consider the drum and mass separately.

 

[Physiona]

Your mgr_i term does not allow for the acceleration of the mass. A more systematic approach is to introduce a variable for the tension in the vertical cable and consider the drum and mass separately.

I agree.