Solving Kinetic Energy with Rotation Around Y Axis

[Ene Dene]

Homework Statement

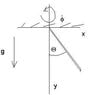
The rod of length 2a swings and it rotates [itex]\dot{\phi}[/tex]. Find kinetic energy.

The Attempt at a Solution

I know how to find kinetic energy if we have rotation just in xy plane, but I'm having a problem to understand how to do it with rotation around y axis.

If we have rotation in xy plane:
$$x_{cm}=asin(\theta)$$
$$y_{cm}=acos(\theta)$$
$$\dot{x}_{cm}=acos(\theta)\dot{\theta}$$
$$\dot{y}_{cm}=-asin(\theta)\dot{\theta}$$
$$E_{kin}=\frac{1}{2}m(\dot{x}_{cm}^2+\dot{y}_{cm}^2)+\frac{1}{2}m\cdot\frac{1}{12}(2a)^2\dot{\theta}^2$$
$$E_{kin}=\frac{2}{3}m\dot{\theta}^2$$

For rotation around y, I assume that we have translation component in z direction, and rotation component.
$$z_{cm}=asin(\theta)sin(\phi)$$
Is this correct? (look at the picture)
$$\dot{z}_{cm}=a(cos(\theta)sin(\phi)\dot{\theta}+cos(\phi)sin(\theta)\dot{\phi})$$
$$E_{z}=\frac{1}{2}m\dot{z}_{cm}^2+\frac{1}{2}I_{cm}\dot{\phi}^2$$.
Rotation part of $E_{z}$ bothers me, maybe I have to multiply it by $(lsin(\theta))^2$.

 

[Ene Dene]

Is this ok:

$$E=\frac{1}{2}(\dot{x}_{cm}^2+\dot{y}_{cm}^2+\dot{z}_{cm}^2)+\frac{1}{2}I_{cm}(\dot{\theta}^2+\dot{\phi}^2)$$

?

 

[Ene Dene]

I have successfully solved the problem by my self, so no need for an answer.