Rotational Dynamics of a ring of mass

[mizzpink]

Homework Statement

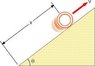
A ring (hollow cylinder) of mass 2.30 kg, inner radius 4.35 cm, and outer radius 5.65 cm rolls (without slipping) up an inclined plane that makes an angle of θ=38.0°, as shown in the figure attached.

At the moment the ring is at position x = 1.95 m up the plane, its speed is 3.00 m/s. The ring continues up the plane for some additional distance and then rolls back down. It does not roll off the top end. How much further up the plane does it go?

Homework Equations

Krot=1/2Iw^2 where I is moment of inertia [I=mr^2]
Kcm=1/2mv^2 where v is the speed of the centre of mass
Ug=Mgh
w=rv [using the outer radius?]
I think the moment of inertia should be I=1/2m(Rinner^2 + Router^2) since it is a hollow cylinder.

The Attempt at a Solution

I used the conservation of energy to formulate: Krot + Kcm + Ug = Ug

Where the left side is at position x and the right side is at the new position that we want to find.

so the height on the right side is what is needed to find and from that we get how far it has moved from position x and then subtract it from x to get the difference.


I think I am approaching the question correctly but there may be some where I am going wrong and I have tried this 3 times already only to get 3 different answers that are all wrong. Thank you very much for your help in advance.

 

[aniketp]

As far as I think you are quite right in your approach. Just check if the rotational inertia you have taken is
I =0.5*M(R₁²+R₂²)
Here R₁ and R₂ are inner and outer radii resp.

 

[mizzpink]

As far as I think you are quite right in your approach. Just check if the rotational inertia you have taken is
I =0.5*M(R₁²+R₂²)
Here R₁ and R₂ are inner and outer radii resp.

I am sure that is the correct formula since I looked it up. The only problem is if I am using the angle correctly. I think that I am using the angle wrong. For Ug, the height h should it be what x is or I should include the angle since x is the hypotenuse. So the height should actually be 1.95sin38. Is that correct? Where else would I use the angle?

 

[Doc Al]

For a change in distance along the incline = x, there is a corresponding change in height h = x sin(theta).

In order to comment on your answers, we need to see exactly what you did.

(Hint: Express the total KE in terms of translational speed.)

 

[aniketp]

I am sure that is the correct formula since I looked it up. The only problem is if I am using the angle correctly. I think that I am using the angle wrong. For Ug, the height h should it be what x is or I should include the angle since x is the hypotenuse. So the height should actually be 1.95sin38. Is that correct? Where else would I use the angle?

I think the angle would figure only in the gravitational potential energy since the velocity is given in the direction of the inclination.

 

[mizzpink]

Never mind I got it myself. I was wrong in the very beginning.

The formula should be Krot+Kcm=Ug. Since energy is conserved meaning that final energy minus initial energy is zero in other words final=initial.

The final is the graviatational potential energy since it is stopped and at a high point above the ground and there is no motion at that point. The initial energy is all motion so it is the total kinetic energy which is rotational KE plus translational KE.

You don't need the x-value at all. I also had the formula for angular speed wrong. It should be w=v/r where r is the outer radius.

Thank you for your help everyone.