A cylinder of snow rolls down a hill gathering more snow -- calculate its speed

[guv]

Homework Statement

cylinder rolls down a hill

Relevant Equations

$mgh = \frac{1}{2} mv^2 + \frac{1}{2} I \omega^2$

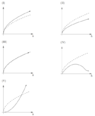
A snow cylinder with an initial radius $R$ rolls without slipping down a tall hill with constant slope. As
it rolls, snow sticks onto the cylinder which makes its radius slowly increase. The amount of gathered
snow is proportional to the distance the snow cylinder has traveled. Consider the following graphs
which represent arbitrary units on the $y$-axis which will be specified according to the problem. (Note:
For graph III, the arrow lies directly on top of the dotted line).

If the dotted line represents the speed of the cylinder if the snow was not sticky, which of the following
graphs represents the speed of the cylinder if the snow sticks to the cylinder, as described above?

The answer says it's Graph III and gives the following explanation,
ince the object is rolling without slipping, we have the relationship $v = \omega r$. Applying energy conservation allows us to write that
$mgh = \frac{1}{2} mv^2 + \frac{1}{2} I \omega^2 = \frac{1}{2} mv^2 + \frac{1}{2} \beta m R^2 (\frac{v}{r})^2$
$v \propto \sqrt{h}$
From this analysis, it is evident that the changing radius of the cylinder does not actually effect
the velocity it rolls down with.

I have some doubt about the given answer. We know that the CM speed is only dependent on the geometry of the object, let the rotational inertia be $I = \beta m R^2$, for cylinder $\beta = \frac{1}{2}$, for a ring it's $\beta = 1$.

Now we can think of the original cylinder having $\beta = \frac{1}{2}$, if snow does not stick to the cylinder, the final CM speed is
$v = \sqrt{ \frac{2 H}{g (1 + \beta)}} = \sqrt{ \frac{4 H}{3g }}$

If the snow sticks to the cylinder without slipping, we can consider the snow form rings on the cylinder whose $\beta = 1$. This should change the overall rotational inertia of the snow object and slows it down.

Let me know how you think about this. Thanks,

 

[kuruman]

First off, the final speed of a cylinder of constant radius rolling down an incline does not depend on the radius but only on $\beta$ which is $\frac{1}{2}$. If you increase the diameter of the cylinder by sticking it into a thin tube that has $\beta=1$, you get a cylinder of more mass but $\beta$ is still $\frac{1}{2}$ for the composite object. The given answer uses that as the basis for saying that the correct answer is III. Let's look at this answer some more.

Stated differently the argument is that, if you race solid cylinders of different masses, and radii down an incline, they will reach the bottom with the same speed and at the same time. If the final speed is the same regardless of mass and radius, the snow cylinder gathering mass and radius should be no different from any other rolling cylinder, hence the answer is III.

That is faulty reasoning. Here is why. Consider racing a fixed-radius cylinder (FRC) against the snow-gathering cylinder (SGC). How do their instantaneous accelerations compare assuming rolling without slipping?

Answer
The FRC has higher acceleration than the SGC. That's because the snow that is picked up is initially at rest and finally moves at the angular velocity of the rim. The change in angular momentum relative to the ground of a mass element $dm$ is effected by a torque exerted on it by the cylinder. By Newton's third law, the accelerating element $dm$ exerts an equal and opposite (decelerating) torque on the cylinder. Thus, the fact that the SGC has to pick up and accelerate snow is the cause for slowing it down relative to the FRC. The graph that best describes this is II.

 

[erobz]

If we ignore that the center of mass is not traveling parallel to the slope as a simplification, I think you want to try to re-express conservation of energy as:

$$ m_o g h_o = \frac{1}{2} m(s) v(s)^2 + \frac{1}{2}I(s) \omega (s)^2 + m(s) g h(s) $$

where $s$ is the coordinate originating at the top of the slope, parallel to the slope.

At least that is what I would try, maybe I'm missing something...

 

[guv]

First off, the final speed of a cylinder of constant radius rolling down an incline does not depend on the radius but only on $\beta$ which is $\frac{1}{2}$. If you increase the diameter of the cylinder by sticking it into a thin tube that has $\beta=1$, you get a cylinder of more mass but $\beta$ is still $\frac{1}{2}$ for the composite object. The given answer uses that as the basis for saying that the correct answer is III. Let's look at this answer some more.

Stated differently the argument is that, if you race solid cylinders of different masses, and radii down an incline, they will reach the bottom with the same speed and at the same time. If the final speed is the same regardless of mass and radius, the snow cylinder gathering mass and radius should be no different from any other rolling cylinder, hence the answer is III.

That is faulty reasoning. Here is why. Consider racing a fixed-radius cylinder (FRC) against the snow-gathering cylinder (SGC). How do their instantaneous accelerations compare assuming rolling without slipping?

Answer
The FRC has higher acceleration than the SGC. That's because the snow that is picked up is initially at rest and finally moves at the angular velocity of the rim. The change in angular momentum relative to the ground of a mass element $dm$ is effected by a torque exerted on it by the cylinder. By Newton's third law, the accelerating element $dm$ exerts an equal and opposite (decelerating) torque on the cylinder. Thus, the fact that the SGC has to pick up and accelerate snow is the cause for slowing it down relative to the FRC. The graph that best describes this is II.

kuruman, this is a more reasonable answer without doing the detailed calculation.

 

[kuruman]

At least that is what I would try, maybe I'm missing something...

I think you missed specifying what system you are considering for conserving energy. You need to include all the snow that is picked up from the initial height $h_0$ to the final height $h_f$. The initial potential energy should not just be $m_0gh_0$ but should include the potential energy of all the snow that is to be picked up. In any case, I am not sure that you can claim mechanical energy conservation. When masses stick together and move as one, you have an inelastic collision that does not conserve energy. This appears to be the case here.

 

[erobz]

I think you missed specifying what system you are considering for conserving energy. You need to include all the snow that is picked up from the initial height $h_0$ to the final height $h_f$. The initial potential energy should not just be $m_0gh_0$ but should include the potential energy of all the snow that is to be picked up. In any case, I am not sure that you can claim mechanical energy conservation. When masses stick together and move as one, you have an inelastic collision that does not conserve energy. This appears to be the case here.

Yeah I figured I missed something ( I always do). I plotted it and there appears to be some funny business that maybe is explained by what you mention. Dependencies on initial height of the mass, the initial mass ect... Anyhow the for a certain set of parameters there appears to be a maximum $\beta$, you can vary the parameters to get it back in line, but I agree that its goofy. Here are a couple plots:

Notice the funny business in the last plot where $\beta$ in increased to $0.7 \rm{\frac{kg}{m}}$. The numerator is going negative there in until $s$ increases to a certain value ( as far as I can tell ). Thats telling me that for a certain $\beta$ and set of inital conditions, it wont even start rolling, that can't be correct...

Back to the drawing board.

 

[kuruman]

What expression are you using for the moment of inertia? It seems to me that both the radius and the mass are a function of $s$. It is given that $m(s)=m_0+\beta s.$ To find $r(s)$ consider adding to the cylinder mass $dm$ in the form of a cylindrical tube of thickness $dr$ and radius $r$. Then $$\begin{align} & \beta~ds=dm=\rho dV=\rho(2\pi r)(dr)L=\frac{m_0}{\pi r_0^2~L}(2\pi r)( dr)L=\frac{m_0}{ r_0^2}2rdr \nonumber \\
&\implies \frac{m_0}{ r_0^2} \int_{r_0}^{r}2rdr = \beta \int_0^s ds \implies r^2=r_0^2\left(1+\frac{\beta s}{m_0} \right).
\nonumber \end{align}$$Thus, $$I(s)=\frac{1}{2}mr^2=\frac{1}{2}\frac{(m_0+\beta s)^2}{m_0} r_0^2.$$

 

[erobz]

What expression are you using for the moment of inertia? It seems to me that both the radius and the mass are a function of $s$. It is given that $m(s)=m_0+\beta s.$ To find $r(s)$ consider adding to the cylinder mass $dm$ in the form of a cylindrical tube of thickness $dr$ and radius $r$. Then $$\begin{align} & \beta~ds=dm=\rho dV=\rho(2\pi r)(dr)L=\frac{m_0}{\pi r_0^2~L}(2\pi r)( dr)L=\frac{m_0}{ r_0^2}2rdr \nonumber \\
&\implies \frac{m_0}{ r_0^2} \int_{r_0}^{r}2rdr = \beta \int_0^s ds \implies r^2=r_0^2\left(1+\frac{\beta s}{m_0} \right).
\nonumber \end{align}$$Thus, $$I(s)=\frac{1}{2}mr^2=\frac{1}{2}\frac{(m_0+\beta s)^2}{m_0} r_0^2.$$

I was using this for the angular term:

$$ \frac{1}{2} I(s) \omega (s)^2 = \frac{1}{2}\left( \frac{1}{2} m(s) R(s)^2 \right) \left( \frac{v(s)}{R(s)}\right)^2 = \frac{1}{4} m(s) v(s)^2 = \frac{1}{4} \left( m_o + \beta s \right) v(s)^2 $$

 

[haruspex]

That is faulty reasoning. Here is why.

Another way of demonstrating it is to suppose that instead of each extra layer of snow accreting to the outside of the cylinder it forms its own little cylinder in parallel. Thus the cylinder moves as in the nonstick case, while the little snow cylinders arrive with successively lower speeds, having not rolled as far.

 

[kuruman]

Another way of demonstrating it is to suppose that instead of each extra layer of snow accreting to the outside of the cylinder it forms its own little cylinder in parallel.

Instead of a little cylinder in parallel wouldn't you have a thin-walled tube in parallel of almost the same radius and a greater $I/(mr^2)$ ratio which would make the comparison unfair?

 

[haruspex]

Instead of a little cylinder in parallel wouldn't you have a thin-walled tube in parallel of almost the same radius and a greater $I/(mr^2)$ ratio which would make the comparison unfair?

Yes, but as against that you would then have to treat the original cylinder has having a larger radius but still the same moment of inertia. That would increase its acceleration.

My thinking was that since the acceleration of a uniform cylinder does not depend on its radius, the constant radius cylinder and the parallel little cylinder have the same acceleration as in the accreting case.
However, I now see that only works if they have the same density.

When masses stick together and move as one, you have an inelastic collision that does not conserve energy.

I don't think that applies here. The point of contact with the ground is instantaneously at rest, so there is no sudden change in velocity for the newly attached snow.

 

[jbriggs444]

I think you missed specifying what system you are considering for conserving energy. You need to include all the snow that is picked up from the initial height $h_0$ to the final height $h_f$. The initial potential energy should not just be $m_0gh_0$ but should include the potential energy of all the snow that is to be picked up. In any case, I am not sure that you can claim mechanical energy conservation. When masses stick together and move as one, you have an inelastic collision that does not conserve energy. This appears to be the case here.

The rolling and picking up snow action looks mechanical energy conserving to me. Nothing inelastic going on. We ditch one energy conserving constraint and pick up a different energy conserving constraint. No sudden jerks or vibrations to dissipate mechanical energy.

 

[erobz]

As for the potential energy of the snow on the ramp that is being picked up along the way; that would be accounted for if I removed the simplification that the center of mass was moving parallel to the slope, correct?

 

[jbriggs444]

As for the potential energy of the snow on the ramp that is being picked up along the way; that would be accounted for if I removed the simplification that the center of mass was moving parallel to the slope, correct?

I am not sure that I follow.

The vertical position of the center of mass of the snow changes when it goes from being a layer on the slope to a roll about the cylinder. One would not expect everything to cancel neatly in a way that is independent of the slope angle.

 

[erobz]

I am not sure that I follow.

The vertical position of the center of mass of the snow changes when it goes from being a layer on the slope to a roll about the cylinder. One would not expect everything to cancel neatly in a way that is independent of the slope angle.

The way I have it set up the center of mass as the radius grows would follow $h(s) + R(s) \cos \alpha$ is what I'm thinking, so the PE of the ball and all the snow its picked up would be at position $s$:

$$ PE(s) = m(s) g \left( h(s)+R(s) \cos \alpha \right) $$

Does that account for the PE of the picked up snow laying on the ramp? I was initially ignoring that, maybe that is the source of the unexpected behavior in post #6. I probably work it in later, and redo the plots.

 

[jbriggs444]

The way I have it set up the center of mass as the radius grows would follow $h(s) + R(s) \cos \alpha$ is what I'm thinking, so the PE of the ball and all the snow its picked up would be at position $s$:

$$ PE(s) = m(s) g \left( h(s)+R(s) \cos \alpha \right) $$

Does that account for the PE of the picked up snow laying on the ramp?

Wait a bit. You are taking the height of the snow, $h(s)$ and not multiplying it by $\cos \alpha$ and then taking the radius of the snowly cylinder, $R(s)$ and multiplying that by $\cos \alpha$. Is that not backward?

Worth asking: Where is your zero point for this calculation?

Edit: I think I get half of it. You are using a zero point on the slope where a perpendicular drawn from the center of the cylinder would intersect. That explains that $\cos \alpha$ multiplier on the shell radius. But it does not explain the lack of a factor of $\cos \alpha$ on the height of the snow layer.

It looks like you are trying to compute the potential energy of the snowy shell based on the sum of the height to which the shell is lifted free of the ground by the snow beneath and on the height of the shell's own center of gravity above its bottom edge.

 

[erobz]

Looking more carefully I think its needs more massaging, because the center of mass is not above $h(s)$, but that is my general direction.

 

[jbriggs444]

View attachment 329208

Looking more carefully I think its needs more massaging, because the center of mass is not above $h(s)$, but that is my general direction.

That diagram looks nothing like my mental picture of the situation. The snow makes a layer on the ground, not a triangle. It has a potential energy when laying on the ground. It has a differrent potential energy when wrapped around the cylinder.

However, I do agree with your formula for the potential energy of the snow wrapped around the cylinder now that I understand how you are using $h(s)$

 

[erobz]

That diagram looks nothing like my mental picture of the situation. The snow makes a layer on the ground, not a triangle. It has a potential energy when laying on the ground. It has a differrent potential energy when wrapped around the cylinder.

However, I do agree with your formula for the potential energy of the snow wrapped around the cylinder now that I understand how you are using $h(s)$

The triangle is the slope its rolling down. I'm not giving physical dimension to the laying snow, other than its mass. I'm just imagining the cylinder is uniformly accreting mass, and its radius is growing accordingly.

Let me save you future headaches. Any time I present a model it's an introductory physics level of abstraction.

 

[erobz]

$s$ is to the point of tangency. I think that the CM being offset is not much of an issue after all. The height directly under the COM $H(s)$ is equivalent to $h(s)+ R(s) \cos \alpha$ upon closer inspection.

I'm a bit slow at seeing these relationships.

 

[kuruman]

I see another complication in the assumed relation $v=\omega~r$. It is valid for rolling without slipping but only if the rolling radius is constant. Here is why.

We have the definitions $$s=r~\theta~;~~v=\frac{ds}{dt}~;~~\omega=\frac{d\theta}{dt}$$and from post #7, $$r=\sqrt{\frac{m_0+\beta s}{m_0}}r_0.$$ It follows that $$\begin{align}\omega= & \cancel{\frac{d}{dt}\left(\frac{s}{r}\right)=v\frac{d}{ds}\left(\frac{s}{r}\right)=v\frac{d}{ds}\left[ s\left( \sqrt{\frac{m_0+\beta s}{m_0}}r_0 \right)^{-1} \right] }\nonumber \\
& =\cancel{\frac{v}{r_0} \sqrt{\frac{m_0}{m_0+\beta s}}\left[1-\frac{\beta s}{2(m_0+\beta s)} \right]} \nonumber \\
& =\cancel{ \frac{v}{r} \left[1-\frac{\beta s}{2(m_0+\beta s)} \right]}.
\nonumber \end{align}$$Clearly, $\omega =v/r$ only when $\beta = 0.$

On edit
This is incorrect. To put it simply, I should have used $ds=r~d\theta$ and then divide by $dt$. The relation $v=\omega~r$ holds at all times. Sorry about that.

 

[erobz]

I see another complication in the assumed relation $v=\omega~r$. It is valid for rolling without slipping but only if the rolling radius is constant. Here is why.

We have the definitions $$s=r~\theta~;~~v=\frac{ds}{dt}~;~~\omega=\frac{d\theta}{dt}$$and from post #7, $$r=\sqrt{\frac{m_0+\beta s}{m_0}}r_0.$$ It follows that $$\begin{align}\omega= & \frac{d}{dt}\left(\frac{s}{r}\right)=v\frac{d}{ds}\left(\frac{s}{r}\right)=v\frac{d}{ds}\left[ s\left( \sqrt{\frac{m_0+\beta s}{m_0}}r_0 \right)^{-1} \right] \nonumber \\
& =\frac{v}{r_0} \sqrt{\frac{m_0}{m_0+\beta s}}\left[1-\frac{\beta s}{2(m_0+\beta s)} \right] \nonumber \\
& = \frac{v}{r} \left[1-\frac{\beta s}{2(m_0+\beta s)} \right] .
\nonumber \end{align}$$Clearly, $\omega =v/r$ only when $\beta = 0.$

Ok, so is subbing that relationship in for $\omega$ an issue as far as the kinetic energies are concerned?

 

[kuruman]

Ok, so is subbing that relationship in for $\omega$ an issue as far as the kinetic energies are concerned?

I would think so.

 

[erobz]

I would think so.

Because they are operating under the assumption of constant $R$ in the derivation?

 

[kuruman]

Because they are operating under the assumption of constant $R$ in the derivation?

Yes, because $v=\omega r$ is valid only when $r$ is constant. The usual derivation is
$s=r\theta$
Taking the time derivative and using the product rule,
$v=\dfrac{ds}{dt}=\theta \dfrac{dr}{dt}+r \dfrac{d\theta}{dt}.$
When $r$ is constant,
$v=0+r \dfrac{d\theta}{dt}=r\omega.$

 

[erobz]

Yes, because $v=\omega r$ is valid only when $r$ is constant. The usual derivation is
$s=r\theta$
Taking the time derivative and using the product rule,
$v=\dfrac{ds}{dt}=\theta \dfrac{dr}{dt}+r \dfrac{d\theta}{dt}.$
When $r$ is constant,
$v=0+r \dfrac{d\theta}{dt}=r\omega.$

Ok, but this should just make what I would predict using $v = r \omega$ an overshoot, or wouldn't you go that far? I mean, having the radius change is not adding energy to the system.

 

[kuruman]

Ok, but this should just make what I would predict using $v = r \omega$ an overshoot, or wouldn't you go that far? I mean, having the radius change is not adding energy to the system.

Sure, but that's a qualitative argument. I thought you wanted to be quantitative and compare $v(s)$ with $\beta = 0$ against $v(s)$ when $\beta \neq 0$. To be quantitative and be correct, you have to have to correct relation between $v$ and $\omega.$

 

[erobz]

Sure, but that's a qualitative argument. I thought you wanted to be quantitative and compare $v(s)$ with $\beta = 0$ against $v(s)$ when $\beta \neq 0$. To be quantitative and be correct, you have to have to correct relation between $v$ and $\omega.$

I’m fine with chipping at it a bit. I don’t wan’t to get too bogged down right away such that I completely stall. Re-forming the kinetic energies seems like a problem of its own.

However, if you want to present the full solution, it won’t hurt my feelings. I’ll probably be asking questions to finish it out regardless.

 

[erobz]

@kuruman well, you put the bug in my head. My thoughts are that the center of mass moves on a curved trajectory:

For the velocity of the center of mass $\frac{dl}{dt}$ I find:

$$ dl^2 = ds^2 + dr^2 $$

$$ \implies \frac{dl}{dt} = \sqrt{ 1 + \left( \frac{dr}{ds} \right)^2 } \frac{ds}{dt} $$

Then for the translational kinetic energy:

$$ KE_{trans.} = \frac{1}{2} m(s) \left( \frac{dl}{dt}\right)^2 =\frac{1}{2} m(s) \left( 1 + \left( \frac{dr}{ds} \right)^2 \right) v(s)^2 $$

Then to get $\frac{dr}{ds}$ we begin with the mass:

$$ \rho \pi L r^2 = \rho \pi L r_o^2 + \beta s $$

$$ \implies 2 \rho \pi L r \frac{dr}{ds} = \beta $$

$$ \implies \frac{dr}{ds} = \frac{\beta}{2 \rho \pi L} \frac{1}{r} $$

Next sub that result into the translational kinetic energy with: $r^2 = r_o^2 + \frac{\beta}{\rho \pi L} s$

$$ KE_{trans.} = \frac{1}{2} m(s) \left( 1 + \left( \frac{\beta}{2 \rho \pi L } \right)^2 \frac{1}{ r_o^2 + \frac{\beta}{\rho \pi L} s} \right) v(s)^2 $$
Is this a step in the right direction?

 

[jbriggs444]

@kuruman well, you put the bug in my head. My thoughts are that the center of mass moves on a curved trajectory:
[...]
$$ KE_{trans.} = \frac{1}{2} m(s) \left( \frac{dl}{dt}\right)^2 =\frac{1}{2} m(s) \left( 1 + \left( \frac{dr}{ds} \right)^2 \right) v(s)^2 $$

Is this a step in the right direction?

You are attempting to solve with calculus? Why?

You can write down a valid energy balance and read off the velocity for any position on the slope from that.

 

[erobz]

You are attempting to solve with calculus? Why?

You can write down a valid energy balance and read off the velocity for any position on the slope from that.

But the center of mass velocity is not collinear with the coordinate velocity. The mass is accreting, the center of mass has two orthogonal components of velocity.

This is in response to the complications @kuruman brings up in #21. I haven't locked down how to tackle those, but in trying to do so this became apparent along the way. If we are worrying about correcting angular kinetic energies, we should correct translational kinetic energy as well?

 

[erobz]

For the angular velocity at any instant in time if the wheel is not slipping, I can't see how the relationship is invalid?

$$ \hat{v} = \hat{r} \times \hat{\omega} = | \hat{r} | ~ |\hat{\omega}| \sin \theta = r \omega \sin \theta \hat s = v(s) \hat s $$

I think the angular kinetic energy is simply as it was:

$$KE_{rot.} = \frac{1}{4} m(s) v(s)^2 $$

and it was the translational energy that needed to be adjusted?

 

[kuruman]

I will be silent on this for a short period of time while I organize and LaTeX my thoughts along a parallel line. Please stay tuned.

 

[jbriggs444]

But the center of mass velocity is not collinear with the coordinate velocity. The mass is accreting, the center of mass has two orthogonal components of velocity.

This is in response to the complications @kuruman brings up in #21. I haven't locked down how to tackle those, but in trying to do so this became apparent along the way. If we are worrying about correcting angular kinetic energies, we should correct translational kinetic energy as well?

If we make the [factually incorrect] assumption that we are dealing with a rolling cylinder then splitting up the total energy into translation and rotation is trivial, regardless of the curvature of the track of the center of mass. We have an instantaneous center of rotation, a moment of inertia relative to that center and we know the energy that is embodied in that rotation. So we know the rotation rate. So we know the state of motion of every body-fixed point on the rolling shape.

Life is more difficult if we shift from the hypothetical cylinder to a more realistic archimedean spiral. The moment of inertia is trickier. The local curvature of the slope-facing surface of the spiral is more difficult to calculate. One would want that to compute the velocity with which the point of contact is advancing down the slope.

 

[erobz]

If we make the [factually incorrect] assumption that we are dealing with a rolling cylinder then splitting up the total energy into translation and rotation is trivial, regardless of the curvature of the track of the center of mass. We have an instantaneous center of rotation, a moment of inertia relative to that center and we know the energy that is embodied in that rotation. So we know the rotation rate. So we know the state of motion of every body-fixed point on the rolling shape.

So, it seems to me like #32 is OK under the [factually incorrect] simplification of a rolling cylinder.
I see I mixed up some things, #32 is not ok.

Life is more difficult if we shift from the hypothetical cylinder to a more realistic archimedean spiral. The moment of inertia is trickier. The local curvature of the slope-facing surface of the spiral is more difficult to calculate. One would want that to compute the velocity with which the point of contact is advancing down the slope.

We have to stop somewhere or (I think you will agree) there practically is no end to this.