Rotational motion and conservation of energy problem

[haydn]

Homework Statement

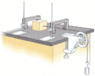
The sliding block has a mass of 0.800 kg, the counterweight has a mass of 0.460 kg, and the pulley is a hollow cylinder with a mass of 0.350 kg, an inner radius of 0.020 m, and an outer radius of 0.030 m. The coefficient of kinetic friction between the block and the horizontal surface is 0.250. The pulley turns without friction on its axle. The light cord does not stretch and does not slip on the pulley. The block has a velocity of 0.820 m/s toward the pulley when it passes through a photogate.

(a) Use energy methods to predict its speed after it has moved to a second photogate, 0.700 m away.

Homework Equations

KE_T = (1/2)mv²
KE_R = (1/2)Iw²

I for a hollow cylinder = (1/2)M(R₁² + R₂²)

w = omega = angular velocity

The Attempt at a Solution

I know work is equal to the change in kinetic energy so I go:

W = ((1/2)(M₁+M₂)V_f² + (1/2)Iw_F²) - ((1/2)(M₁ + M₂)V_I² + (1/2)Iw² + M₂gs)

and W = -f * s = - (coefficient of friction)M₁gs

s = .7 as given in the problem...

So I substitute that expression for work into the first equation, solve for V_F but the website I'm using is telling me I'm getting the wrong answer... what am I doing wrong?

 

[quantumdude]

and W = -f * s = - (coefficient of friction)M₁gs

That's not right. There is no reason that the work done by friction must equal the change in gravitational potential energy of the object. The Work-Energy Theorem states that the net work done on a system equals the change in total kinetic energy of the system. So we have:

W_{total}=\Delta K_{total}

W_f+W_g=\Delta K_{block}+\Delta K_{pulley}+\Delta K_{counterweight}

-Fs+m_2gs=\frac{1}{2}m_1\left(v_2^2-v_1^2\right)+\frac{1}{2}I\left(\omega_2^2-\omega_1^2\right)+\frac{1}{2}m_2\left(v_2^2-v_1^2\right)

You'll need to relate \omega to v, but other than that this should be a piece of cake. You know everything except v_2.

 

[haydn]

Ok, isn't friction force equal to the coefficient of friction times the normal force though? ..and the normal force of the block = M₁g since it isn't moving vertically?

Thanks for the help by the way, besides that everything is clear now.

 

[quantumdude]

Ok, isn't friction force equal to the coefficient of friction times the normal force though? ..and the normal force of the block = M₁g since it isn't moving vertically?

Yes on both counts.

Thanks for the help by the way, besides that everything is clear now.

No problem!