siifuthun
- 24
- 0
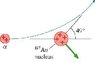
An alpha particle approaches a Au (gold) nucleus with atomic mass number 197 with a speed of 1.5*10^7 m/s. The alpha particle is then scattered 49 degrees from the horizontal at the slower speed of 1.47*10^7 m/s.
In what direction does the Au nucleus recoil below the x-axis (the horizontal) in degrees?
I don't think I'm approaching this problem in the right way. Part B of the question asks with what speed does the Au nucleus recoil, so I thought that once I had the velocity of the nucleus, I could somehow figure out the angle it recoiled at, but I'm not sure if I have to use the force of repulsion to do that.
I also had another similar problem where they tell us the radius of an oxygen atom with atomic mass 16 has a radius of 3.0 fm. and the question asked at what speed would a proton need to be fired toward the oxygen nucleus if it were to have a turning point at 1.20 fm from the surface.
Looking through an example in my book, by using conservation of energy we get:
final kinetic energy (K_f) + final potential energy (U_f) = initial kinetic energy (K_i) + initial potential energy (U_i)
from that i got the expression:
0 + ((q_alpha)(q_Au))/(r_min*4*pi*epsilon_0) = .5m(v_i)^2
So I solve for my v_i using 1.20 fm + 3.0 fm as my r_min. 1.6*10^-19 as my charge for the proton, 16*1.6*10^-19 as the charge of my nucleus, and for the mass I used the mass of the proton (1.67*10^-27).
After calculating it by plugging in the numbers, I got 3.24*10^7 m/s, but it's wrong and I'm not sure if I used the wrong r_min because I tried using just 1.2 fm and and 4.2 fm (converted into meters) but I'm sill not getting the right answer.
If anyone can help, I'd be really grateful, these two problems really confused me. Thanks. I've also attached a picture of the diagram for the problem with the Au nucleus.
In what direction does the Au nucleus recoil below the x-axis (the horizontal) in degrees?
I don't think I'm approaching this problem in the right way. Part B of the question asks with what speed does the Au nucleus recoil, so I thought that once I had the velocity of the nucleus, I could somehow figure out the angle it recoiled at, but I'm not sure if I have to use the force of repulsion to do that.
I also had another similar problem where they tell us the radius of an oxygen atom with atomic mass 16 has a radius of 3.0 fm. and the question asked at what speed would a proton need to be fired toward the oxygen nucleus if it were to have a turning point at 1.20 fm from the surface.
Looking through an example in my book, by using conservation of energy we get:
final kinetic energy (K_f) + final potential energy (U_f) = initial kinetic energy (K_i) + initial potential energy (U_i)
from that i got the expression:
0 + ((q_alpha)(q_Au))/(r_min*4*pi*epsilon_0) = .5m(v_i)^2
So I solve for my v_i using 1.20 fm + 3.0 fm as my r_min. 1.6*10^-19 as my charge for the proton, 16*1.6*10^-19 as the charge of my nucleus, and for the mass I used the mass of the proton (1.67*10^-27).
After calculating it by plugging in the numbers, I got 3.24*10^7 m/s, but it's wrong and I'm not sure if I used the wrong r_min because I tried using just 1.2 fm and and 4.2 fm (converted into meters) but I'm sill not getting the right answer.
If anyone can help, I'd be really grateful, these two problems really confused me. Thanks. I've also attached a picture of the diagram for the problem with the Au nucleus.