Scotch yoke mechanism movement equation

[Lluis]

TL;DR

How to change Scotch yoke mechanism parameters in order to calculate slider movement

Hi,

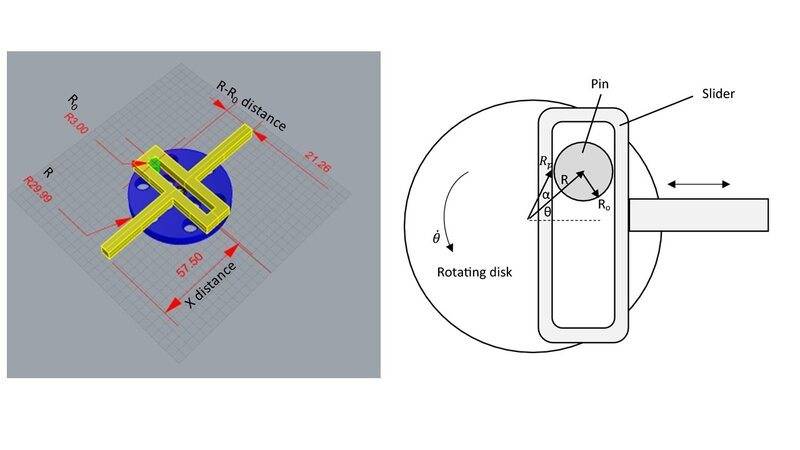
I am not an engineer and sorry in advance if I am not correct with the terms. I design out of curiosity this Scotch yoke mechanism (left image) based on a scheme (right image).

I looked for some equations to find if there is a relation between the R0 , R to R0 distance (which changes during rotation) and the X distance. If for example, I will change the parameters R0 , R to R0 distance and the slider horizontal part/s length/s how it will effect the X distance movement?

Any idea how to calculate it?

Thanks a lot.

 

[jack action]

Assuming the slider is at 0 in the left image, the slider will move from -R to +R (Total: 2R).

The size R0 doesn't affect the stroke distance; it only needs to be large enough to carry the force (depends on the material strength). It's like selecting a bearing for a wheel or a connecting rod: The bearing size doesn't affect the kinematics of the wheel or the connecting rod, it just needs to be large enough to support the load.

Changing the length X doesn't affect the stroke either.
$$\Delta x = R\sin \theta$$
$\Delta x$: Slider displacement
$\theta$: Crank angle (0° when slider is centered as in left image)

 

[Lnewqban]

Welcome!
As explained above, the slider stroke is only modified by R.
As R and the stroke get smaller, the pushing/pulling force of the slider gets bigger (greater mechanical advantage), and vice-verse.

Consider that you need enough X distance to accommodate the guides of the slider without interfering with the rotating disc.