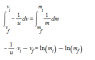Separation of variables - rocket equation

In summary, the conversation is about someone trying to understand how to solve a step in the derivation of Tsiolkovsky's rocket equation. They are having trouble with the use of separation of variables and are seeking clarification on the rules and integration process. The expert summarizes that the integration boundaries should be from final velocity to initial velocity, and explains the change of variables used in the integration process.
  • #1
Januz Johansen
34
1
hello there
Im trying to do a derivation of tsiolkovsky's rocket equation, but i got stuck at the step when i have to use separation of variables (marked with red in the pic), i used maple to solve it, so i could get on with it, but i want to understand what is happening to solve this, so can anyone explain how to solve this step with separation of variables?
Thanks :)
upload_2016-11-27_15-19-15.png
 
Physics news on Phys.org
  • #2
It is exactly what they have done. What step in particular do you have problems with?
 
  • #3
Orodruin said:
It is exactly what they have done. What step in particular do you have problems with?

ok thanks so i have done some right ;)

im having trouble explaining what is happening, or i think i do.
I can explain the first steps, just isolate the variables on each side of the equation.
But what rules are used/how is this integrated (the bordered step)
Thanks :D
upload_2016-11-27_15-59-54.png
 
  • #4
You integrate both sides between the same points. It is essentially making an integration and then making a change of variables.
 
  • Like
Likes Januz Johansen
  • #5
Orodruin said:
You integrate both sides between the same points. It is essentially making an integration and then making a change of variables.
Thanks i see now :D
 
  • #6
Oh, and the integration boundaries on the LHS should be ##v_f## to ##v_i##. In this particular example it does not matter for the result because the integrand is constant. You then make a change of variables to ##m(v)## and use ##m_f = m(v_f)## and ##m_i = m(v_i)##.
 
  • #7
Hello
Do you mean like this?
upload_2016-11-27_16-20-29.png

im not 100% sure what you mean with the change of variables
Again thank you for helping
 

Attachments

  • upload_2016-11-27_16-20-25.png
    upload_2016-11-27_16-20-25.png
    1.5 KB · Views: 593
  • #8
Yes. Consider the integral
$$
\int_{v_f}^{v_i} dv.
$$
Now, you know that ##m## is a function of ##v## so change variables to ##m##. The integral changes to
$$
\int_{m(v_f)}^{m(v_i)} \frac{dv}{dm} dm.
$$
Insert the known differential equation and perform the new integral.
 
  • #9
so i have it like so:
upload_2016-11-27_16-46-29.png

or do i get -1/u*m(vi)-m(vf)?
thank you for your patience and help
 
  • #10
No, you have the wrong integration boundaries in the first integral. They are what I said in my post.
 

Related to Separation of variables - rocket equation

1. What is the rocket equation and why is it important in space travel?

The rocket equation, also known as the Tsiolkovsky rocket equation, is a mathematical equation that describes the motion of a rocket in terms of its mass and the exhaust velocity of its propellant. It is important in space travel because it helps calculate the amount of propellant needed to reach a certain velocity and altitude, and also determines the maximum payload a rocket can carry.

2. How does the separation of variables method apply to the rocket equation?

The separation of variables method is a mathematical technique used to solve differential equations. In the rocket equation, it is used to separate the variables of velocity and mass so that the equation can be solved for each variable independently. This allows for more accurate and efficient calculations for space missions.

3. What assumptions are made in the rocket equation?

The rocket equation assumes a constant mass flow rate and a constant exhaust velocity. It also assumes that the rocket is traveling in a vacuum and is not affected by external forces such as air resistance. These assumptions allow for a simplified model of the rocket's motion.

4. How does the rocket equation account for changes in mass during a space mission?

The rocket equation takes into account the changing mass of the rocket as it burns its propellant. This is done by using the concept of specific impulse, which is a measure of the efficiency of the rocket's engine. As the propellant is burned and expelled, the mass of the rocket decreases, resulting in a change in velocity.

5. Can the rocket equation be applied to all types of rockets?

Yes, the rocket equation can be applied to all types of rockets, including chemical, nuclear, and electric propulsion rockets. However, some modifications may need to be made depending on the specific type of rocket and its propulsion system. Additionally, the rocket equation is most accurate for single-stage rockets, but can still provide useful estimates for multi-stage rockets.

Similar threads

A Separation of variables possible in this problem?
    • Differential Equations
Replies
3
Views
1K
I Separation of Variables, but not equal to constant
    • Differential Equations
Replies
3
Views
1K
I Heat Equation: Solve with Non-Homogeneous Boundary Conditions
    • Differential Equations
Replies
4
Views
1K
I Determining equilibrium solutions to differential equations
    • Differential Equations
Replies
16
Views
914
MHB How can I solve a non-homogeneous equation using substitution?
    • Differential Equations
Replies
1
Views
1K
I Separation of Variables and Integrating over an Interval
    • Differential Equations
Replies
3
Views
1K
I Finish and plot this separation of variables problem
    • Differential Equations
Replies
10
Views
3K
I Quick Change of Variables Question
    • Differential Equations
Replies
15
Views
2K
A Solving a PDE in four variables without separation of variables
    • Differential Equations
Replies
4
Views
2K
Why is the thrust equation same under gravitational force?
    • Introductory Physics Homework Help
Replies
10
Views
695

Hot Threads

Recent Insights

Back
Top