Serge Lang: Inequality Problem

[Cosmophile]

Hello, all. I am reading Serge Lang's "A First Course in Calculus" in order to get a better understanding of the topic. I thought I would read his review of fundamental concepts, and, naturally, it has been a breeze so far. However, I am stumped when trying to work out this problem:

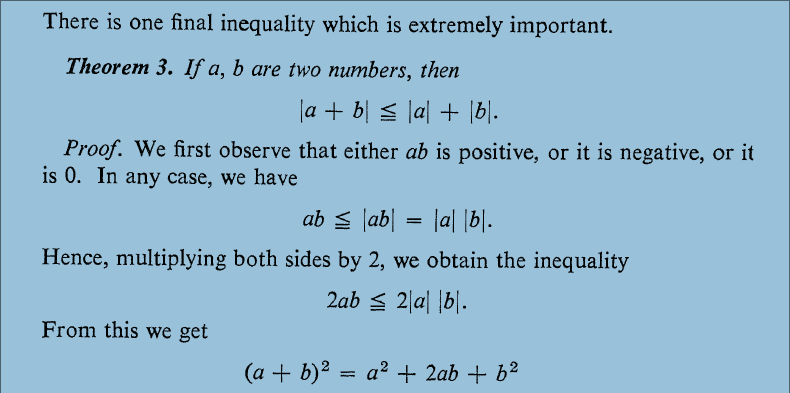
I do not see how 2ab \leq 2|a||b|
turns into (a+b)^2 = a^2 +2ab + b^2

Any help in resolving this is greatly appreciated. I don't want to move on without understanding this bit. It's really bothering me.

Also, I apologize for not adhering to the established template. I didn't see a way to formulate this question in a way that fit the template.

 

[haruspex]

I do not see how 2ab \leq 2|a||b|
turns into (a+b)^2 = a^2 +2ab + b^2

It doesn't turn into that. The second equation is always true. I would have to guess that the use of the first equation comes a bit further on. If that doesn't explain it, please post a longer extract.

 

[Cosmophile]

I stepped away from it for a while (since I posted this) and when I sat down, I realized that it was just a poor execution (in my opinion) on Lang's part. The "from this we get..." confused me into thinking the first could be manipulated into becoming the second. The first was stated because I can use that to say:

(a+b)^2 \leq a^2 +2|a||b| + b^2 <br /> = (|a|^2 + |b|^2)
Square root both sides and voila, you get |a+b| \leq |a| + |b|
which is what we wanted to prove. All I had to do was step away for a bit.