SHM - Pendulum and Mass on a spring

[Shaye]

Homework Statement

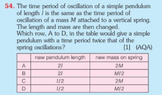
The time period of oscillation of a simple pendulum of length l is the same as the time period of oscillation of a mass M attached to a vertical spring. The length and mass are then changed. Which row, A to D (see attachment), in the table would give a simple pendulum with a time period twice that of the spring oscillations?

Relevant Equations

T = 2π√(l/g): Mass on a pendulum
T = 2π√(m/k): Mass on a spring

I have only be able to write something like:

2x(2π√(l/g)) = 2π√(m/k)
2π is a constant therefore; 2x(√(l/g)) = √(m/k)
You could square both sides; 2^2x(l/g) = (m/k)

But now I'm lost as to how to proceed.

PS- Book answer is B

Thanks

 

[kuruman]

2x(2π√(l/g)) = 2π√(m/k)

Does this look right to you? It says
2*(Pendulum period) = (Spring mass period)
If a father's age is twice that of his son's age, would you write
2*(father' age) = (son's age) ?

Aside from that, I would recommend that you write the new periods using different symbols for the changed length and mass and then take ratios for the periods cancelling quantities that remain unchanged.