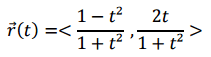Discussion Overview
The discussion revolves around demonstrating that a particle moves along a circumference centered at the origin. Participants explore the mathematical representation of the particle's position vector and its implications for motion along a circular path, including directionality and the occupancy of points on the circumference as a parameter varies.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant presents the position vector and attempts to use the equation x² + y² = r² to show the particle's motion along a circumference.
- Another participant provides algebraic manipulations to confirm that the expression simplifies to 1, indicating the particle's path is indeed circular.
- Some participants note potential typos in the expressions used, particularly regarding the coefficients in the y-coordinate, which could affect the conclusions drawn.
- There is a discussion about determining the direction of the particle's motion as the parameter t increases, with suggestions to analyze the behavior of the functions or relate them to trigonometric identities.
- Participants question whether all points on the circumference are occupied by the particle as t varies from negative to positive infinity, leading to a debate about the implications of the parameterization and the nature of real numbers.
- One participant suggests that certain points, such as (-1, 0), are not occupied by the particle, prompting further exploration of the mathematical conditions that lead to this conclusion.
Areas of Agreement / Disagreement
Participants express differing views on the occupancy of points on the circumference, particularly regarding the point (-1, 0). While some agree that not all points are occupied, others question the reasoning behind this conclusion, indicating that the discussion remains unresolved.
Contextual Notes
Participants highlight limitations in the mathematical expressions used, such as the dependence on the parameter t being real and the implications of approaching infinity. There is also a recognition that certain points cannot be attained based on the parameterization provided.