karush
Gold Member
MHB
- 3,240
- 5
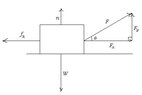
An object wth weight $W$ is dragged along a horizontal plane
by a force acting along a rope attached to the object
If the rope makes an angle $\theta$ with the plane, then the magnitude of the force is
$
\displaystyle
F=\frac{\mu W}{\mu\sin{\theta}+\cos{\theta}}
$
where $\mu$ is a positive constant called the coefficient of friction
and where $$0<\theta\le \pi/2$$ Show that $F$ is minimized when $\tan\theta=\mu$
this was a problem under min/max values. I was going to find F' or try to graph this
in W|F but got a 3d graph which I didn't understand.
Am sure this is a common problem in Physics but it was put in with exercises in Calculus
Anyway curious how this is solved...
by a force acting along a rope attached to the object
If the rope makes an angle $\theta$ with the plane, then the magnitude of the force is
$
\displaystyle
F=\frac{\mu W}{\mu\sin{\theta}+\cos{\theta}}
$
where $\mu$ is a positive constant called the coefficient of friction
and where $$0<\theta\le \pi/2$$ Show that $F$ is minimized when $\tan\theta=\mu$
this was a problem under min/max values. I was going to find F' or try to graph this
in W|F but got a 3d graph which I didn't understand.
Am sure this is a common problem in Physics but it was put in with exercises in Calculus
Anyway curious how this is solved...