SUMMARY
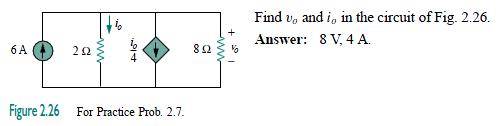
The discussion focuses on solving a circuit problem using Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL). The user initially struggles to relate voltage (v) and current (i) in the circuit but ultimately derives the correct current value of i = 4 A through proper application of KCL and Ohm's Law. The user also clarifies the equivalent resistance of the circuit branches, confirming that the voltage drop across the 2-ohm resistor is equal to v. The final solution is reached by correcting arithmetic errors in the calculations.
PREREQUISITES
- Understanding of Kirchhoff's Current Law (KCL)
- Understanding of Kirchhoff's Voltage Law (KVL)
- Familiarity with Ohm's Law
- Basic circuit analysis techniques
NEXT STEPS
- Study advanced circuit analysis techniques using Thevenin's and Norton's theorems
- Learn about mesh and nodal analysis for circuit simplification
- Explore practical applications of KCL and KVL in real-world circuits
- Review common mistakes in circuit calculations to improve accuracy
USEFUL FOR
Electrical engineering students, circuit designers, and anyone looking to improve their understanding of circuit analysis using KCL and KVL.