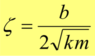Simple harmonic motion - damping introduced
- Thread starter Jozefina Gramatikova
- Start date
Click For Summary
SUMMARY
The discussion centers on solving the equation for time, t, in the context of simple harmonic motion with damping, specifically using the damping coefficient b in the formula. Participants clarify that the equation to solve is e^{-b/(2m)t} = 1/2, leading to the conclusion that taking the natural logarithm of both sides is necessary to isolate t. The final calculated time, t, is approximately 3.05 seconds, based on the correct use of the natural logarithm value ln(2) = 0.693.
PREREQUISITES- Understanding of simple harmonic motion principles
- Familiarity with damping coefficients in physics
- Knowledge of exponential functions and logarithms
- Basic skills in algebraic manipulation of equations
- Study the derivation of the damping coefficient in harmonic motion
- Learn about the effects of damping on oscillatory systems
- Explore the relationship between amplitude and time in damped oscillations
- Investigate advanced topics in differential equations related to harmonic motion
Students and educators in physics, particularly those focusing on mechanics and oscillatory motion, as well as anyone involved in solving differential equations related to damping in harmonic systems.
Similar threads
- · Replies 1 ·
- · Replies 51 ·
- · Replies 11 ·
- · Replies 7 ·
- · Replies 13 ·
- · Replies 5 ·
- · Replies 14 ·