Simple problem:Voltage of capacitors AFTER closing a switch

[easyyy]

Hello guys. Please look at this, it's a VERY SIMPLE problem and I've almost solved it, but sth is not right...

It's a simple problem but i am confused regarding the method that I'm supposed to use to solve this kind of problems. So the problem is:
V1 , V2 , V3 and V4, E1, E2 are given. They are the voltages before closing the switches. We have to find the same voltages V1', V2', V3' and V4' after closing the switches. The values with - ' - are the values AFTER closing the switches.

so, MY WORK UP TO HERE:

I have the following equations:

(1) Q1+Q2+Q3+Q4=Q1'+Q2'+Q3'+Q4 , because the total charge won't change after closing the switches
(2) -E1+V1'+V2'+E2-V3'+V4'=0 , because of the 2nd rule of Kirchoff
(3) Q1 + Q2=Q1'+Q2' (because these two capacitors are in linear connection)

Equations (1) and (3) can be rewritten using that Q=C*V and Q'=C*V' , because the capacity will not change after closing the circuit.
So we have 3 equations and 4 variables (V1' , V2', V3', V4' ). So how am I supposed to find these variables?? Maybe the equation (3) or is not correct, or even the (2) but that's alla I could do...


I would be gratefull if anyone could help because it's not just for this problem, I want to see the way I should work to solve this. Thnx in advance :)
// The circuit is here: as an image:

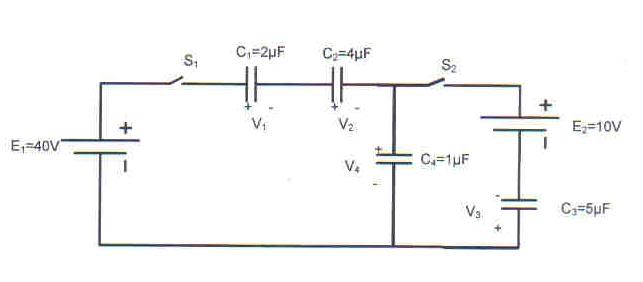
URL is: http://img.photobucket.com/albums/v446/easyyy/circuit.jpg"

 

[Saketh]

When I see capacitors in series or parallel, the first thing I do is rewrite them as a single simplified capacitor. Using your knowledge about capacitors in series or parallel, try simplifying the circuit. It's not necessary, but you'll have fewer variables to think about. Then, after solving for the unknowns in the simplified equations, you can go back and plug in the determined values.

For example, look at the 2uF and 4uF capacitors. You can rewrite them as one capacitor with the equation

\frac{1}{C_1} + \frac{1}{C_2} = \frac{1}{C_{combined}}.

This comes out to 4/3 uF. As you can see, the charge across the combined capacitors is the same as that of the simplified capacitor, so, after solving for the charge, you can go back and plug it back into the un-simplified equations. Start solving for variables after you've simplified the circuit.

It's similar to what you do for resistors, if you've done that already, except that what you do for series and parallel is flipped.

 

[SGT]

...
I have the following equations:

(1) Q1+Q2+Q3+Q4=Q1'+Q2'+Q3'+Q4 , because the total charge won't change after closing the switches
...

Since there are voltage sources in the circuit, when you close the switches there will be currents flowing through the circuit, so there is no conservation of charges.