Understanding Trigonometric Functions: Solving for Length AD

  • Context: High School 
  • Thread starter Thread starter smulc
  • Start date Start date
  • Tags Tags
    Trigonometry
Click For Summary
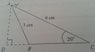
SUMMARY

The discussion centers on calculating the length AD using trigonometric functions, specifically 8sin20° and 8cos70°. The user initially believed both calculations would yield the same result but discovered discrepancies due to their calculator being set to radians instead of degrees. The correct values are 8cos70° = 5.067 and 8sin20° = 7.304, confirming that the calculations are indeed different. Additionally, it is noted that cos70° must be less than 0.5, reinforcing the understanding of trigonometric values in relation to angles.

PREREQUISITES
  • Understanding of basic trigonometric functions (sine and cosine)
  • Familiarity with angle measurement in degrees and radians
  • Ability to use a scientific calculator
  • Knowledge of the unit circle and its properties
NEXT STEPS
  • Learn how to convert between degrees and radians in trigonometric calculations
  • Study the unit circle and its application in solving trigonometric problems
  • Explore the properties of sine and cosine functions for various angles
  • Practice using a scientific calculator effectively for trigonometric functions
USEFUL FOR

Students studying trigonometry, educators teaching mathematical concepts, and anyone needing to solve problems involving angles and lengths using trigonometric functions.

smulc
Messages
33
Reaction score
0
I need to find the length AD. I thought that with the numbers given, and angle A worked out to being 70o there would be two different ways of working length AD out. I thought 8sin20 and 8cos70 would both be acceptable ways of calculating the length but they give different values. Where have I gone wrong?

Thanks.
 

Attachments

  • 20121006_121928.jpg
    20121006_121928.jpg
    8.9 KB · Views: 465
Mathematics news on Phys.org
They don't give different values.
 
My calculator gives 8cos70 = 5.067 and 8sin20 = 7.304.
 
just realized it was in raidians mode. Whoops!
 
smulc said:
My calculator gives 8cos70 = 5.067 and 8sin20 = 7.304.

and you should realize (hopefully quickly) that if cos60o=1/2 then cos70o must be less than half, so there is no way 8cos70o > 5, and similarly with sin20o :wink:
 

Similar threads

High School New solutions to old, historic problems
  • · Replies 2 ·
Replies
2
Views
2K
High School How Can Trigonometry Calculate Distances in Surveying?
  • · Replies 5 ·
Replies
5
Views
3K
High School Finding all possible sums given 2 lists, matched one to one
  • · Replies 2 ·
Replies
2
Views
2K
High School Golden Ratio in Collatz-like sequences
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Why is it important to convert angle units when using trigonometric functions?
  • · Replies 8 ·
Replies
8
Views
2K
High School What are some strategies to prove trigonometric results
  • · Replies 2 ·
Replies
2
Views
1K
High School Calculating trigonometry without calculator?
  • · Replies 8 ·
Replies
8
Views
2K
High School Why Do We Draw Dimensionless Unit Vectors in Diagrams?
  • · Replies 16 ·
Replies
16
Views
4K
High School Compensating for a bias - a simple geometry/algebra problem:
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Adding trig functions with different amplitudes
  • · Replies 5 ·
Replies
5
Views
2K