StephenDoty
- 261
- 0
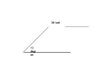
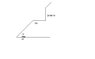
Say I wanted to know how fast I would need to go in a car that weighs 6000lbs that would clear at 20 foot gap in a bridge inclined 10 degrees. Is there a way I can use conservation of energy to find the velocity needed to clear the 20 foot gap?
1/2mv^2=mgh
v^2=2gh
v=sqrt(2gh)
Would I put the 20ft in the h spot? Since I do not know the acceleration of the car I cannot use kinamatics. Any help would be appreciated.
Thank you.
Stephen
1/2mv^2=mgh
v^2=2gh
v=sqrt(2gh)
Would I put the 20ft in the h spot? Since I do not know the acceleration of the car I cannot use kinamatics. Any help would be appreciated.
Thank you.
Stephen