Simplify Tricky Equation for Purely Imaginary C with Complex Constants

[thatboi]

Hey all,
I am currently trying to solve the following equation for C:

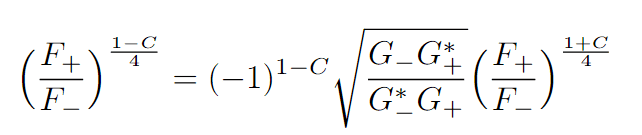
where C is a purely imaginary value, $F_{+}$, $F_{-}$ and $G_{+}$ and $G_{-}$ are all complex valued constants (so $G_{+}^{*}$ just means complex conjugate of $G_{+}$. I am not really sure where to start with isolating C, any advice would be greatly appreciated!

 

[FactChecker]

Take logarithms of both sides and see if you can solve that equation for C.

 

[malawi_glenn]

Let $F_+ /F_- = A$ and $\sqrt{ \dfrac{G_-G_+^*}{G_-^*G_+} } = B$

Your equation is $A^{-C/2} = (-1)^{1-C}B$

Always do simplifications and change of variables, to see what is going on.

 

[phyzguy]

@thatboi , with the two hints given to you above, it is fairly easy to solve for C. Is that working out for you?

 

[thatboi]

@thatboi , with the two hints given to you above, it is fairly easy to solve for C. Is that working out for you?

Thanks for the hints I have already worked it out!

 

[malawi_glenn]

Great!

May I ask where this equation came from?