Simplifying Complex Circuits for Resistance Calculations

[xxkbxx]

Homework Statement

Okay - the picture is attached, but what I need to find is the current and voltage throughout certain points on the circuit. What I need help on is figuring out how to simplify this circuit in order to find resistance.

Homework Equations

Parallel Req = (1/R1 + 1/R2)^-1
Series Req = R1 + R2

The Attempt at a Solution

I know how to combine equations for series and parallel circuits - but what can I do with R4? I need to simplify the circuit, but I know I can't put it in parallel with R5 or R6 since it has resistance in both loops. Is there a way to combine R5 and R6. Let me know please...

 

[denverdoc]

I think R5 and R6 can be combined since you have only the one voltage source, then added to R4.

 

[xxkbxx]

I tried that before, but I was unsure. The eq of R5 and R6 is (1/(R5) + 1/(R6))^-1 Then that would be added to R4, since R4 is in series. Okay, that makes more sense now - I think I have the rest from here!

 

[@/@]

I believe that tou can join the R5/R6 in parallel more the R4 in series to form a "block" with the R4 in parallel with this block

 

[xxkbxx]

I believe that the circuit would be the same as the attachment from R1, R2, and R3 - but the last branch would have R5 and R6 in parallel in the "block" as you called it, in series with R4.

Would my total resistance than be:
Req = R1 + R2 + (1/(R3) + (1/R4) + (1/(1/R5 + R6))

Specifically, how would I add up the resistance of the R5 and R6 Block?

 

[denverdoc]

I tried that before, but I was unsure. The eq of R5 and R6 is (1/(R5) + 1/(R6))^-1 Then that would be added to R4, since R4 is in series. Okay, that makes more sense now - I think I have the rest from here!

Right on.

But just wait til they start adding batteries all over.

 

[denverdoc]

I believe that the circuit would be the same as the attachment from R1, R2, and R3 - but the last branch would have R5 and R6 in parallel in the "block" as you called it, in series with R4.

Would my total resistance than be:
Req = R1 + R2 + (1/(R3) + (1/R4) + (1/(1/R5 + R6))

Specifically, how would I add up the resistance of the R5 and R6 Block?

I think that's close call R4+1/(1/R5+1/R6)=Z
Req=R1 + R2 + 1/(1/r3+1/z) is what I see.

 

[@/@]

I believe that the circuit would be the same as the attachment from R1, R2, and R3 - but the last branch would have R5 and R6 in parallel in the "block" as you called it, in series with R4.

Would my total resistance than be:
Req = R1 + R2 + (1/(R3) + (1/R4) + (1/(1/R5 + R6))

Specifically, how would I add up the resistance of the R5 and R6 Block?

R1+{1/R3+[(1/R5+1/R6)+R4]}+R2
R1+ \{ \frac{1}{R3} + (( \frac{1}{R5}+ \frac{1}{R6} )+ R4) \} + R2

 

[Curious3141]

Homework Statement

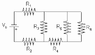
Okay - the picture is attached, but what I need to find is the current and voltage throughout certain points on the circuit. What I need help on is figuring out how to simplify this circuit in order to find resistance.

Homework Equations

Parallel Req = (1/R1 + 1/R2)^-1
Series Req = R1 + R2

The Attempt at a Solution

I know how to combine equations for series and parallel circuits - but what can I do with R4? I need to simplify the circuit, but I know I can't put it in parallel with R5 or R6 since it has resistance in both loops. Is there a way to combine R5 and R6. Let me know please...

Teach you a little trick to make these problems easier.

When two resistors R and r are in parallel, use the notation (R || r) to express the effective resistance. The two parallel lines '||' have an obvious meaning.

When two resistors R and r are in series, just add them up as usual, i.e. the effective resistance is R + r.

Now, your objective is to reduce the diagram in stages to a single resistance. Just forget about the mathematics and express everything in this notation at first.

When you reduce a pair of resistors, immediately redraw the diagram with the effective resistance of the pair as a single resistor. Just stick with the notation.

So, you'd begin : R5 is in parallel with R6, the effective resistance is (R5 || R6). That is now in series with R4, the effective resistance is now (R5 || R6) + R4, and so forth.

When you finally finish the reduction, you should get the effective resistance of the entire circuit (R) as :

R = {[(R5 || R6) + R4] || R3} + R2 + R1

(Be sure to bracket each pair of resistances as you reduce them, to avoid making a mistake).

Looks complicated, but it isn't really when you work through it yourself. It becomes a lot easier if you keep drawing the intermediate steps in the reduction with single resistances replacing the pairs you've reduced.

Now just apply the relation R || r = (1/R + 1/r)^(-1) = (Rr)/(R+r), while taking care with the brackets, and you've got the effective resistance of the circuit.

 

[denverdoc]

Slick, I like that. Improves legibility, reduces chance for error, avoids the need to make subs as I did...

 

[Curious3141]

Slick, I like that. Improves legibility, reduces chance for error, avoids the need to make subs as I did...

Wait till you see how legible they make (otherwise) complicated complex impedance problems!