noelll
- 13
- 0
Hi there,
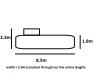
I am doing a simulation of a free-fall lifeboat trajectory into the ocean and there is a part where i need to get the volume of the lifeboat to obtain its buoyancy force.
Buoyancy force is proportional to the immersed volume of the body and this volume can be obtain by integrating the immersed cross-section area along the length of the boat(I am using Simpson's rule 1/3 for this).
2. Homework Equations
Buoyancy force = Density*gravity*volume
Question i would like to ask, do i need to find the volume in a time-step manner, currently the ideal i have in mind is at each meter of the lifeboat length i will obtain a cross-section and after reaching the end of the lifeboat length which is 8.5 m i add up all the cross-section area? however i do not know how to do it.
i tried doing the simpson's rule. But i could only get a single number.
I hope anybody out there could help me, really need your help, thank you so much!
Best Regards,
Noel
Homework Statement
I am doing a simulation of a free-fall lifeboat trajectory into the ocean and there is a part where i need to get the volume of the lifeboat to obtain its buoyancy force.
Buoyancy force is proportional to the immersed volume of the body and this volume can be obtain by integrating the immersed cross-section area along the length of the boat(I am using Simpson's rule 1/3 for this).
2. Homework Equations
Buoyancy force = Density*gravity*volume
Question i would like to ask, do i need to find the volume in a time-step manner, currently the ideal i have in mind is at each meter of the lifeboat length i will obtain a cross-section and after reaching the end of the lifeboat length which is 8.5 m i add up all the cross-section area? however i do not know how to do it.
The Attempt at a Solution
i tried doing the simpson's rule. But i could only get a single number.
Code:
%INPUTS
L = 0; %lower limit
U = 8.5; % upper limit
n = 40; % number of segments
Length = 1;
Breath = 3;
Height = 2.3;
density= 1.025;
g = 9.81;
func = @(x) (Breath * Height);
h = (U-L)/n;
st4 = 0;
st2 = 0;
for i = 2:h:n
st4 = st4 + 4*func(i);
end
for i = 3:h:n
st2 = st2 + 2*func(n);
end
buoyancy_force = (density*g)*(h/3*(func(1)+st4+st2+func(i)));
disp (buoyancy_force)
fprintf('step %.3f\n',i);
disp (st4)
disp (st2)I hope anybody out there could help me, really need your help, thank you so much!
Best Regards,
Noel
Last edited: