SIN Contest Water Tank in a Moving Vehicle Question

[daga2222]

Homework Statement

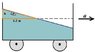
Audrey McLaughlin has a vehicle with a built-in rectangular swimming pool. The pool is 2.4m long, 1.4m wide, and is partly filled with water to a constant depth of 1.2m as shown. Calculate the minimum additional height, h, to avoid water spillage when the vehicle maintains a steady forward acceleration of 4.9m/s^2 on a horizontal road. Ignore and "sloshing" motion associated with changes in acceleration. Answer in cm.

Data: dimensions of tank are 2.4m long and 1.4m wide, and the water is filled to a height of 1.2m

The question is asking about the additional height that the tank must have to not have any water spillage.

Options:

A) 120cm

B) 107cm

C) 84cm

D) 60cm

E) 54cm

Homework Equations

Net force?

Maybe conservation of energy equations?

The Attempt at a Solution

The only way I can think of to solve this question is to find the angle of the net force acting on the water. I did this using components method, adding mg + (m x acceleration of truck (4.9m/s^2))

The angle i found allowed me construct a right angle triangle with which I used 1.2m or half the length of the tank as a side to calculate the opposide side or height. The answer i got was 120cm. (After subtracting 1.2m of water originally.)

If anyone could help me with this question or verify the answer I would appreciate it.

 

[TSny]

Hello, daga2222. Welcome to PF!

I don't think 120 cm is the right answer. Sounds like you generally have the right approach. Using half the length of the tank for the base of your triangle sounds good. Could you explain in more detail how you arrived at the angle for the triangle?

 

[daga2222]

I used components method. I took the inverse tangent of 0.5 (ratio of 4.9/9.8) to get 26.6 degrees or so. Using this angle I couldn't get any of the listed answers, so I used the complementary angle of 63.4. This allowed me to find the opposite side of the triangle (height) which was 2.4m. Subtracting by 1.2m the original height, I got 120cm. This was the only way I could reproduce one of the possible answers.

When I use tan26.6 x 1.2 I get 0.6m. Is that correct? I discarded the answer because it's lower than the original height of the water, but maybe the base of the triangle is at the surface of the water?

 

[haruspex]

Let the angle to the vertical of the net force from the truck on the water be theta. What do you get for tan theta? How are you then calculating h from this? Your method looks right, but you have not posted enough detail to say where your error is.

 

[daga2222]

I posted a reply with more information. I don't get what else you are specifically looking for?

 

[TSny]

What did you get for the height of your triangle when the angle is 26.6 degrees?

 

[daga2222]

0.6m

I did tan 26.6 x 1.2m.

 

[TSny]

Is that one of the answers?

 

[daga2222]

Yes, but the water was originally 1.2m high so I thought it wasn't a proper answer. I guess the base of the triangle is on the surface of the water?

 

[TSny]

Doesn't it look something like this? Isn't 60 cm for h ok?

 

[daga2222]

Ahh that makes so much more sense. I was originally drawing the triangle from the base of the tank. The height of the triangle is the additional height that the water moves. Thanks so much!