SUMMARY
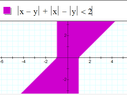
The discussion focuses on sketching the region defined by the inequality |x-y| + |x| - |y| ≤ 2. Participants analyze the problem using the triangle inequality and break it down quadrant by quadrant. They establish that |x - y| ≤ 1 is a key conclusion, indicating that the relationship between x and y is constrained within a specific range. The conversation emphasizes the importance of considering each quadrant to fully understand the solution space.
PREREQUISITES
- Understanding of absolute value inequalities
- Familiarity with the triangle inequality
- Basic knowledge of Cartesian coordinates and quadrants
- Experience with sketching regions defined by inequalities
NEXT STEPS
- Study the properties of absolute value functions in inequalities
- Learn how to apply the triangle inequality in various mathematical contexts
- Explore methods for sketching regions defined by multiple inequalities
- Investigate point-symmetry in mathematical solutions
USEFUL FOR
Mathematics students, educators, and anyone interested in understanding geometric interpretations of inequalities in the Cartesian plane.