tjosan
- 32
- 2
- Homework Statement
- A slab is placed on two supports. At one edge, a weight is added. How large can the weight be before the slab tips over? The slab weighs 300 kg, and the density is constant. See image for attempted solution and a drawing of the slab.
- Relevant Equations
- F_1*d_1=F_2*d_2
Hi,
My attempted solution is in the image:
I choose the edge on the left side, but the solution should be similar on both sides (just substitute C for A).
(I missed to multiply by "g" in F_2.)
Is this the correct way of thinking? I'm not sure about the distance "D".
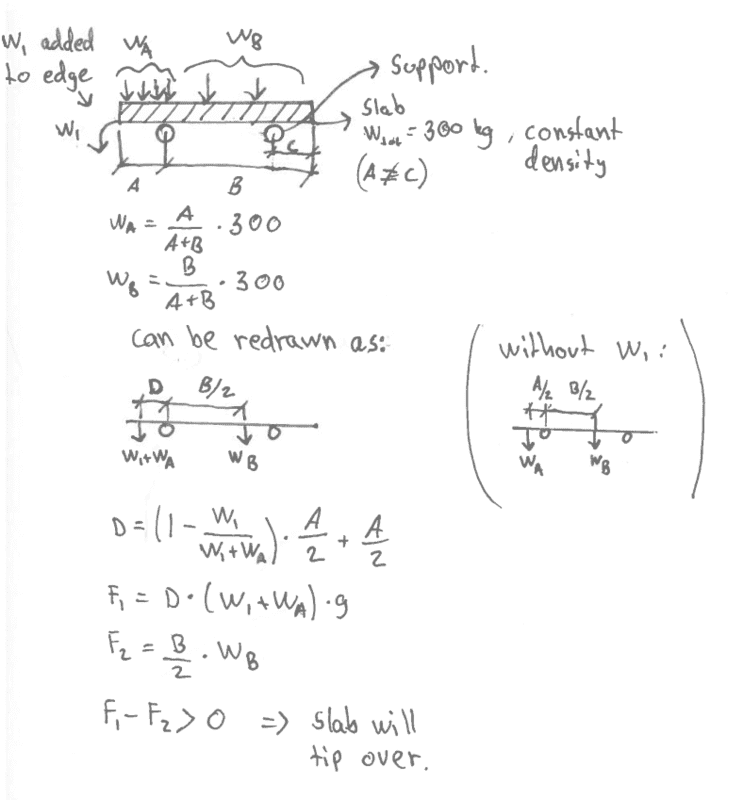
My attempted solution is in the image:
I choose the edge on the left side, but the solution should be similar on both sides (just substitute C for A).
(I missed to multiply by "g" in F_2.)
Is this the correct way of thinking? I'm not sure about the distance "D".