- #1
melpomenne
- 9
- 0
1. A uniformly loaded crate of weight 1000N is held at rest on an inclined place. A gradually increasing force P is applied horizontally as shown. If coefficient of friction, u, = 0.2, determine whether the crate first slides or topples and the least force required
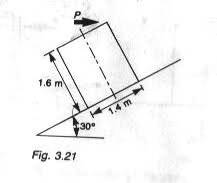
I am unable to find the least force required. please help me solve this - the answer is 726 N
3. Reaction R = 1000 cos 30 + P sin 30
F = uR
P cos 30 - F -mg sin 30 = 0
I am unable to find the least force required. please help me solve this - the answer is 726 N
3. Reaction R = 1000 cos 30 + P sin 30
F = uR
P cos 30 - F -mg sin 30 = 0