SUMMARY
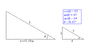
The discussion centers on calculating the distance covered by Eddie "The Eagle" Edwards on a ski jump with a horizontal velocity of 20 m/s and a landing slope gradient of 37 degrees. Participants clarify that the 90 m measurement is not directly relevant to the calculation. The key equations discussed include the trajectory of the skier as a parabolic function and the slope of the landing as a linear function, leading to the conclusion that the intersection of these two functions determines the distance along the slope. The conversation emphasizes the importance of separating horizontal and vertical motion in projectile problems.
PREREQUISITES
- Understanding of projectile motion and its equations
- Knowledge of linear equations and slopes
- Familiarity with parabolic trajectories in physics
- Basic skills in algebra and functions
NEXT STEPS
- Study the equations of motion for projectiles in parametric form
- Learn how to derive the equations of parabolas from projectile motion
- Explore the concept of slope in linear equations and its applications
- Practice solving problems involving the intersection of linear and parabolic functions
USEFUL FOR
Students studying physics, particularly those focusing on projectile motion and mathematical modeling, as well as educators looking for examples of applying algebra to physics problems.