Slope of a mountain ridge (Gradient)

[Lambda96]

Homework Statement

Write $h(r)=H$ as $y(H,x)$

and

Calculate steepest and flattest slope with $|| \nabla h(r) ||$

Relevant Equations

none

Hi

I am not quite sure if I have calculated the whole task correctly, since I am not sure whether I have solved task e correctly and unfortunately have problems with task f

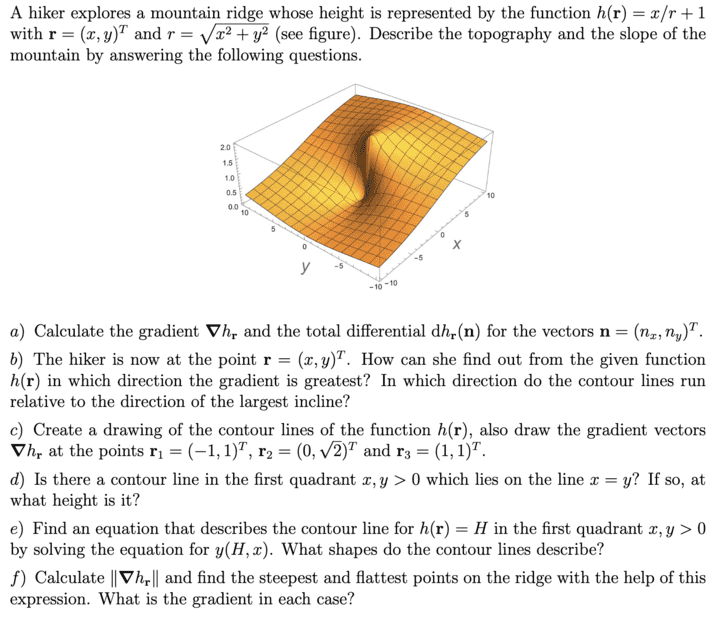
The function h(r) looks like this $h(r)=\frac{x}{\sqrt{x^2+y^2}}+1$

I got the following for the gradient

$\nabla h(r)=\left(\begin{array}{c} -\frac{x^2}{(x^2+y^2)^{\frac{3}{2}}} + \frac{1}{\sqrt{x^2+y^2}} \\ - \frac{xy}{(x^2+y^2)^{\frac{3}{2}}} \end{array}\right)$

and the plot for contour lines looks like this:

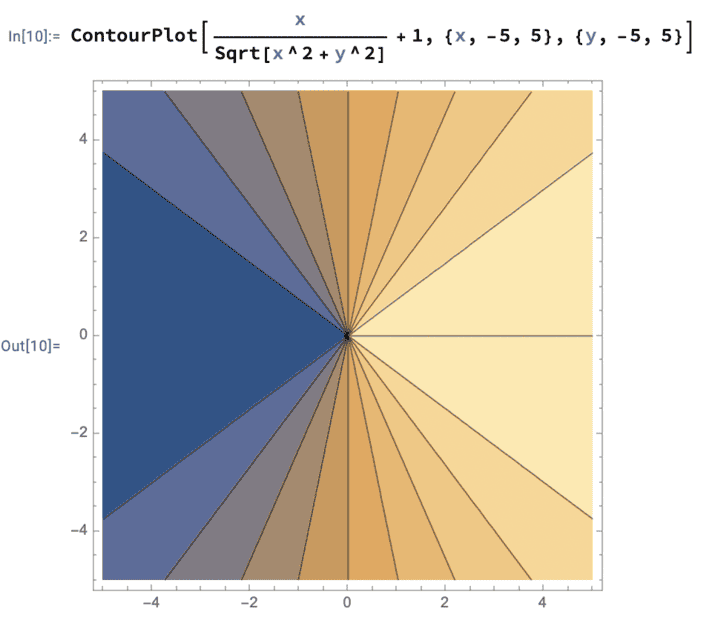
$\textbf{Task e}$

I then solved the equation $h(r)=H$ for y as follows $y(H,x)= \sqrt{\frac{x^2}{(H-1)^2}-x^2}$ The shape of the contour lines in the first square are all straight lines

I could only see that they are straight lines from the contour lines plot and not from the equation above, did I calculate y(H,x) incorrectly?

$\textbf{Task f}$

The amount of the gradient should be calculated as follows

$|| \nabla h(r) ||=\sqrt{\biggl( -\frac{x^2}{(x^2+y^2)^{\frac{3}{2}}} + \frac{1}{\sqrt{x^2+y^2}} \biggr)^2 + \biggl( -\frac{xy}{(x^2+y^2)^{\frac{3}{2}}} \biggr)^2}$

and then got the following

$|| \nabla h(r) ||= \sqrt{\frac{y^2}{(x^2+y^2)^2}}$

For the steepest and flattest slope, I have to insert the points into the above equation where the gradient is zero, so $\nabla h(r)= \left(\begin{array}{c} 0 \\ 0 \\ \end{array}\right)$ I have calculated these points with mathematica and if I have not made a mistake, unfortunately only complex solutions come out

Have I made a mistake in calculating the steepest or flattest ascent or can I only do this with $|| \nabla h(r) ||$?

 

[pasmith]

In polar coordinates $x = r \cos \theta, y = r \sin \theta$ for $-\pi \leq \theta < \pi$ we have $$h(r, \theta) = 1 + \cos \theta.$$ It follows that $$\nabla h = -\frac{\sin \theta}{r}\mathbf{e}_\theta = - \frac{y}{r^2}(-y/r, x/r)^T$$ and $$\|\nabla h\| = \frac{|\sin \theta|}{r} = \frac{|y|}{x^2 + y^2}.$$ This is zero whenever $y = 0$ (and is undefined at the origin).

I suspect the fact that $\nabla h$ has degenerate (ie, non-isolated) zeros is confusing whatever algorithm Mathematica is using to solve $\nabla h = 0$. Think before you compute!

 

[Lambda96]

Thank you pasmith for your help

Where the gradient is zero, there is either a maximum and minimum, the magnitude of the gradient is then also zero.

As you have already written, this would be the case for $y=0$. If I now insert $y=0$ into the equation $h(r)$, I get $h(x,0)=\frac{x}{\sqrt{x^2}}+1$ and is either zero for $x<0$ or 2 for $x>0$

So the steepest slope would be 2 and the flattest 0

 

[pasmith]

Thank you pasmith for your help

Where the gradient is zero, there is either a maximum and minimum, the magnitude of the gradient is then also zero.

As you have already written, this would be the case for $y=0$. If I now insert $y=0$ into the equation $h(r)$, I get $h(x,0)=\frac{x}{\sqrt{x^2}}+1$ and is either zero for $x<0$ or 2 for $x>0$

So the steepest slope would be 2 and the flattest 0

"Steepest slope" is where the magnitude of the gradient is maximal, and "flattest slope" is where the magnitude of the gradient is minimal. You can see from my earlier post that $\|\nabla h\|$ increases without limit as $r \to 0$ for $y \neq 0$ and is zero when $y = 0$.

 

[haruspex]

This is zero whenever y=0 (and is undefined at the origin).

Do you mean "(except that it is undefined at the origin)"?

 

[Lambda96]

Thank you pasmith for your help