Snell's Law: Parallel Polarization Derivation

[Brianrofl]

Hi, I have a plane-wave incident upon a planar interface that is perpendicularly polarized with an electric field directed out of the page in the y-hat direction, perpendicular to the x-z plane of incidence. An image of the incident plane:

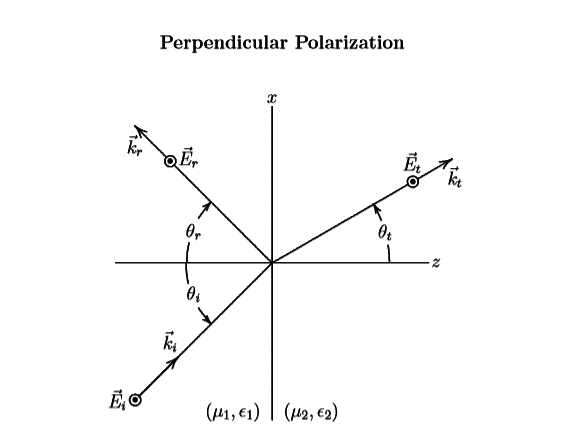
I'm also given the general expressions for the incident, reflected, and transmitted waves for perpendicular polarization:

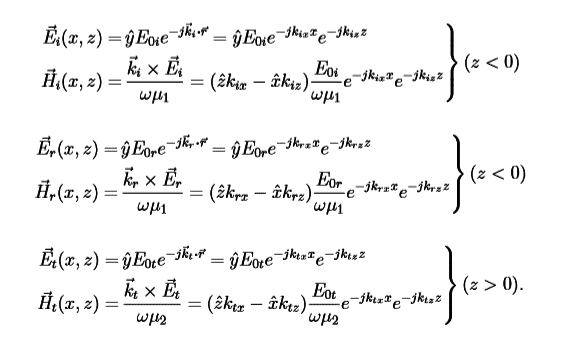
Some relevant eqns (just maxwell equations and solutions):

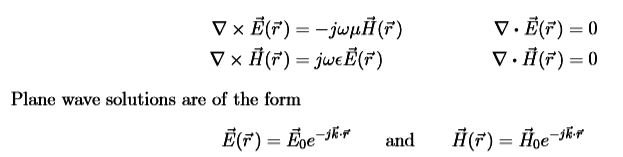
Alright, so what I need to do here is obtain the expressions of E for a parallel polarization, rather than perpendicular. The solution should come from duality, which I assume also comes from maxwell equations.

What I do know is that the solution is obtained from the perpendicular incidence of H. Do I simply use the above maxwell equation Del x H = jweE(r), and take the curl of each H(x,z) equation to obtain E for the parallel case?

I'm not looking for the solution, but if someone could just point me in the right direction here I'd appreciate it.

 

[RUber]

When you change to parallel polarization, are you changing your planar reflector from the x-y plane to the y-z plane, or are you changing your expression of
E from $\vec E_{inc}(x,z) = \hat y E_0 f(x,z)$ to $\vec E_{inc}(y,z) = \hat x E_0 g(y,z)$?
Make that clear first, then see what changes need to occur in your forms. I think it is easier to change the vector forms rather than the geometry.