So the statement sin(n+1)pi/2 = cos(n)pi/2 is true by this property.

SVXX · Feb 17, 2011

Question - Find the Fourier series for f(x) = |cos(x)| in the interval (-π, π).
Right, I attempted the question and the integration that followed. I'm having trouble in the integration itself..
Firstly I found that f(x) is an even function, so the sine term(b_n) of the Fourier expansion would be zero and that I can use a property of integration to write

$gif.latex?a_0%20=%20\frac{1}{\pi}%20\int_{-\pi}^{\pi}f(x)dx.gif$

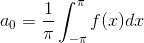as

$gif.latex?a_0%20=%20\frac{2}{\pi}%20\int_{0}^{\pi}f(x)dx.gif$

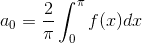and similarly so for a_n.

$%20=%20\frac{1}{\pi}%20\int_{0}^{\pi}[cos(n-1)x%20\hspace{1mm}%20+%20\hspace{1mm}%20cos(n+1)x]dx.gif$

$frac{1}{\pi}[\frac{sin(n-1)x}{n-1}]_0%20^\pi%20+%20\frac{1}{\pi}[\frac{sin(n+1)x}{n+1}]_0%20^\pi.gif$

I computed a₀ to be zero, but the trouble is, I'm getting a_n to be zero too, and if that is so, there will be no Fourier series! Could someone please point out my mistake?

uart · Feb 17, 2011

Hints :

1. One period of |cos(x)| extends from -pi/2 to pi/2. Check your limits.

2. Beware divide by zero.

SVXX · Feb 18, 2011

Thanks for the hints...I figured out what I was doing wrong in the integration. I had to break the intervals at pi/2 as |cos(x)| = cos(x) for 0 < x < pi/2 and = - cos(x) for pi/2 < x < pi.
I referred a popular book from the college library today which proved me correct. But what I don't understand is the last part of the solution that was given in that book...it stated that sin(n+1)pi/2 = cos(n)pi/2...how is this so?

uart · Feb 18, 2011

SVXX said:

Thanks for the hints...I figured out what I was doing wrong in the integration. I had to break the intervals at pi/2 as |cos(x)| = cos(x) for 0 < x < pi/2 and = - cos(x) for pi/2 < x < pi.
I referred a popular book from the college library today which proved me correct. But what I don't understand is the last part of the solution that was given in that book...it stated that sin(n+1)pi/2 = cos(n)pi/2...how is this so?

The complementary relation between sin and cos tells us that sin x = cos (pi/2 - x) and visa versa.

So sin (n+1)pi/2 = cos (pi/2 -(n+1)pi/2) = cos (-n pi/2).

Now since cos is an even function then cos (-n pi/2) = cos (n pi/2).

So the statement sin(n+1)pi/2 = cos(n)pi/2 is true by this property.

Discussion

Similar threads