Solenoid Magnetic Field calculation

[UMath1]

I am confused about how the magnetic field of a solenoid is calculated in this image.

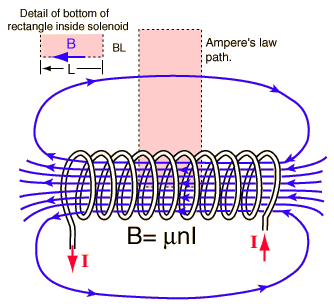
Why is only the current going into the page included in calculating the magnetic field? Shouldn't the field be twice the amount calculated because there is a magnetic field generated by the part of the turns the bottom with current going out of the page? And I don't understand why the vertical components of the path are taken to be zero. Although it is said that the field is perpendicular, the diagram shows that there is a portion of the field parallel to the vertical path.

 

[Hesch]

The diagram is to be found here:

https://www.google.dk/search?q=sole...UIBygB&biw=1920&bih=946#imgrc=hFGPz8dNvVVwhM:

If you go to the homepage:

http://hydrogen.physik.uni-wuppertal.de/hyperphysics/hyperphysics/hbase/magnetic/solenoid.html

there is an explanation.

Have you read it?

 

[UMath1]

Yes. But it doesn't answer my question.

 

[Hesch]

Why is only the current going into the page included in calculating the magnetic field? Shouldn't the field be twice the amount calculated because there is a magnetic field generated by the part of the turns the bottom with current going out of the page?

Ampere's law is used.
It says that only the current passing through the area of the rectangle is to be included in the calculation:

∫_circ H ⋅ ds = N * I

And I don't understand why the vertical components of the path are taken to be zero.

They are not taken to be zero, but they cancel each other due to symmetrical reasons. The formula is only valid as for the center of the solenoid.

The upper side of the rectangle is assumed to be so far away, that it has no influence, so this horizontal component is taken to be zero.
You are the one to sketch the rectangle.

 

[UMath1]

Yes I understand that. But if you use ampere's law that way, the circular winding of the wire seems to have no bearing on the field inside the wire. I thought that the field inside the solenoid is increased because of the winding if the wire.

 

[Hesch]

But if you use ampere's law that way, the circular winding of the wire seems to have no bearing on the field inside the wire. I thought that the field inside the solenoid is increased because of the winding if the wire.

I'm not using Ampere's law that way, just using Ampere's law.

If you want a "bearing", you must use Biot-Savart's law. It doesn't need symmetry, infinite length of the solenoid, and so on.

Biot-Savart is accurate in case of finite length of the solenoid. Ampere is an approximation.