SUMMARY
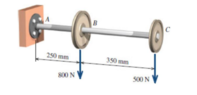
The discussion focuses on using the singularity function to determine deflections in beam mechanics. Participants emphasize the necessity of expressing the moment as a function of the variable x, leading to the integration of the moment equation to derive deflections. The equation used is \(EI \frac{d^2y}{dx^2} = M(x)\). Additionally, it is highlighted that a constant moment must be included in \(M(x)\) to account for vertical reactions and moments at point A under equilibrium conditions.
PREREQUISITES
- Understanding of singularity functions in solid mechanics
- Familiarity with beam deflection theory
- Knowledge of moment equations in structural analysis
- Proficiency in calculus, specifically integration techniques
NEXT STEPS
- Study the application of singularity functions in beam deflection problems
- Learn about the derivation of moment equations for various beam loading conditions
- Explore the concept of vertical reactions and equilibrium in structural analysis
- Investigate advanced integration techniques relevant to solid mechanics
USEFUL FOR
Students and professionals in civil engineering, mechanical engineering, and structural analysis who are focused on beam stress and deflection calculations.