Solidworks thermal simulation: is this logical?

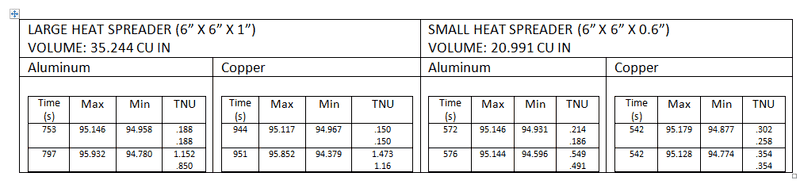
[_Bd_]

I just ran 2 simulations on Solidworks, same assembly, same initial conditions on all pieces, pretty much I "Cloned" the thermal study and just changed one piece

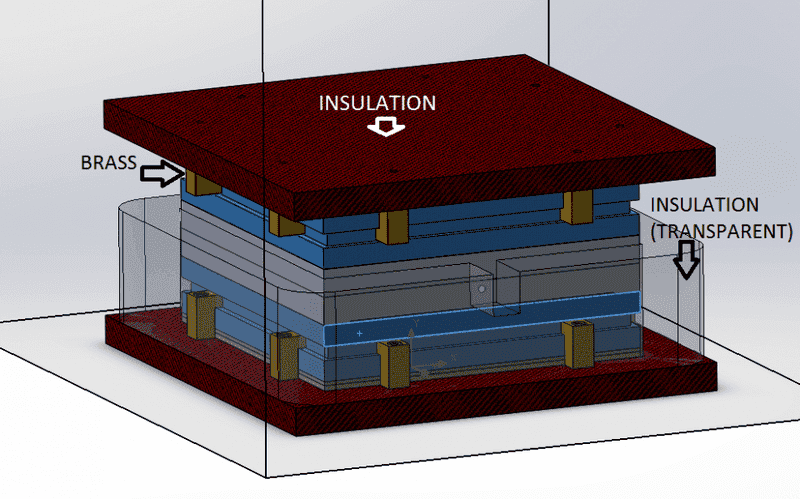
So,
from the assembly above you can see the materials for most pieces, the 2 grey pieces in the center are 2 aluminum plates with a hole in the center and a "probe" at the middle of that hole (this is a temperature-reference point).
For additional clarification, see the cross-section below

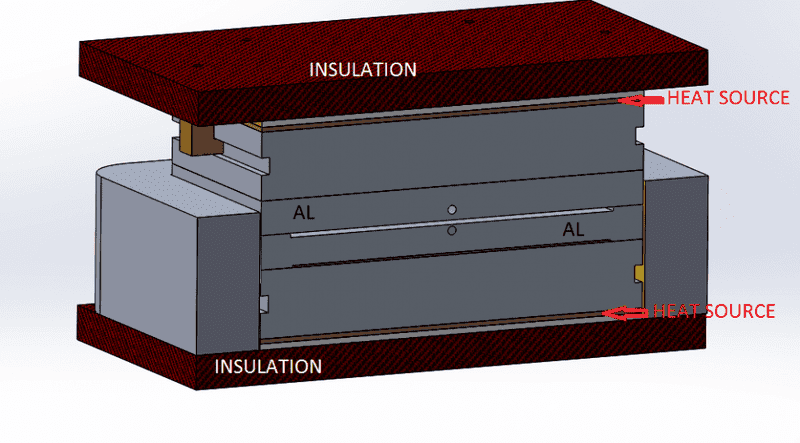
Now, the heat sources are 325 Watts of power each, and the pieces in question (highlighted above) are the only "variant" in both studies, as you can see heat transfers from the heat source to this big block then it transfer to the aluminum pieces.

The purpose of my simulation was to find out what material is better for this big block, Copper or Aluminum?

The obvious answer should be copper, it has less heat capacity (less energy to heat up) and more conductivity (faster response time). *Please feel free to correct me if I'm wrong*

Now, based on those facts about Al vs Cu, it should be obvious that with all other variables the same, the copper should heat up much faster than the Aluminum right?

Well, the Solidworks simulation shows the following results:

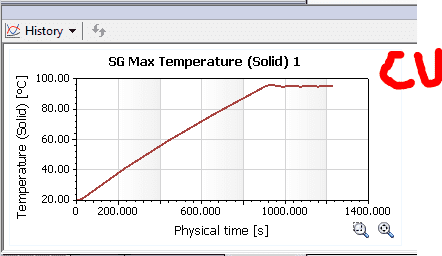
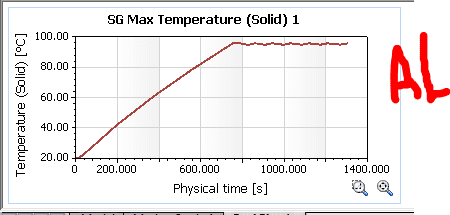
As you can see from the results, the copper seems to be a little more steady (the heat source shuts down after a point reaches 95°C)
However, what really puzzles me is the fact that copper takes roughly 150 extra seconds to heat up to 95, which shouldn't be the case right?

Can someone please help me make sense of this? should I dump solidworks simulation ?

 

[Mech_Engineer]

Like any FEA package, Solidworks simulation is a number cruncher so in the end it will only give you numbers based on inputs. It can't tell you if the solution it gives you is "wrong" though, it's up to you to apply engineering judgment.

The parameter most relevant to you application is in fact a sort of "volume heat capacity" between the two materials in question, because the time it takes them to heat up will depend on the product of their density and specific heat capacity.

Copper specific heat capacity: 384.4 J/(kg*K)
Copper density: 8.96 gm/cm^3

Aluminum specific heat capacity: 904 J/(kg*K)
Aluminum density: 2.7 gm/cm^3

It turns out that while copper is an excellent thermal conductor, it also is relatively dense; aluminum on the other hand is a pretty good thermal conductor but also is low in density. When you compare the product of each material's specific heat capacity and density, volume-for-volume copper takes more energy to heat up to a particular temperature.

Comparison:
Copper Volume Heat Capacity: 3.44 J/(cm^3*K)
Aluminum Volume Heat Capacity: 2.4 J/(cm^3*K)

So in fact for a fixed power input and part geometry, copper will take longer to heat up because it has a 43.5% higher "volume heat capacity" than aluminum. Double check your material properties being used but I think the result makes intuitive sense.

This result would be different however, if you made the copper part smaller to take advantage of its superior thermal conductivity while reducing the total mass of copper in the system.

 

[_Bd_]

That makes perfect sense! thank you. I completely forgot to think in terms of volume rather than mass. . .for some reason I assumed the same mass since it was the same piece. . Thanks!

 

[_Bd_]

Hey Guys,
I'ma bump this thread with another question regarding the same model (or a very similar one).

In the OP you can see the two chunks of metal (named heat spreader)

Those pieces are 6"x6"x1", with a whopping volume of around 35 cubic inches
For experiment's sake I decided to change those pieces to be 6x6x0.6", this drops the volume to 21 cu in.

I ran the simulation again, and this time the Copper heated up around 15 seconds faster than aluminum. Based on what Mech_Engineer said it shouldn't be the case (and it makes perfect sense). However, here it seems there's other things playing a role and I'd like some help figuring them out. The only thing I can think of is that there is more surface area to volume ratio in smaller pieces. I looked over at my old heat transfer book and saw the "Flow over an isothermal plate" examples, however none of the examples seem to consider the plate's material. The only driving factor is the fluid properties, based on this there shouldn't be a difference in heat lost to ambient wether its aluminum or copper (This doesn't sound quite right tho).
Anyways, here are the results:
Note the two rows are for the top half and bottom half

 

[Mech_Engineer]

What kind of boundary conditions do you have applied in the model, and where are they applied?

Edit: To be more thorough in your analysis, I would look at a cross-section of the part and compare the temperature distribution of the aluminum vs copper, it might be you'll find a dynamic effect where the copper is conducting heat more efficiently in a particular direction, but its hard to know with only a "heating time" parameter.