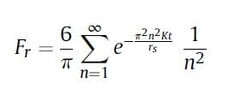IanM
- 2
- 0
This is my first time posting so forgive me if I have it in the wrong place,
i'm trying to find a solution to the following that I can stick into either excel or a VBA script. It has been 25 years since I looked at any serious maths and I'm stumped. I can find and digest e^-(n^2y) but can't work out the n^-2 addition. Happy to be walked though the steps if it helps me get a better understanding, for those interested it is part of a solution to determine the ability for gas to flow though a porous medium
View attachment 6510
Cheers
Ian
i'm trying to find a solution to the following that I can stick into either excel or a VBA script. It has been 25 years since I looked at any serious maths and I'm stumped. I can find and digest e^-(n^2y) but can't work out the n^-2 addition. Happy to be walked though the steps if it helps me get a better understanding, for those interested it is part of a solution to determine the ability for gas to flow though a porous medium
View attachment 6510
Cheers
Ian