Solve for Smallest Theta for Slider to Reach A

[stinlin]

Homework Statement

k = 40 N/m
mass of slider = 200 g
EDIT r = 0.3 m
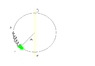
Hoop is VERTICAL, undeformed length of the spring is when spring is in position AB, slider NOT attached to spring.

Find smallest value for theta such that the slider will pass through D and reach A (see picture).

Homework Equations

s = r*theta
1/2 k * x^2
mgh
1/2 mv^2

The Attempt at a Solution

I set up the initial and final energy equations but couldn't figure out how to solve them. =P

Denoting @ as theta:

mgr(1-cos(@)) + 1/2*k(r@)^2 = mg*2r

After plugging in numbers and rearranging, I found:

mgcos(@) + 0.0018277@^2 = 1.962

I don't know how to solve for @ in that equation. Also, in the spring term of 1/2kx^2, I replaced x by r@ (s = r@) and multiplied @ by pi/180 to convert to radians for that term.

 

[radou]

Until you post a clearar diagram, I doubt anyone will be able to entirely check your equations.

 

[stinlin]

That's the diagram in my book really...It's a vertical circle with a slider and a spring attached to point A (slider NOT attached to spring)

And my equation is wrong I discovered, but have NO clue what the right one is.