chwala
Gold Member
- 2,833
- 426
- Homework Statement
- see attached
- Relevant Equations
- quadratic/cubic equations
Kindly see the questions and its mark scheme below;
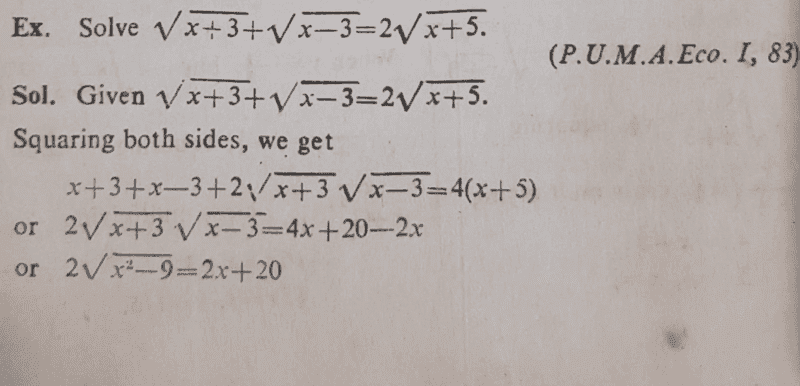
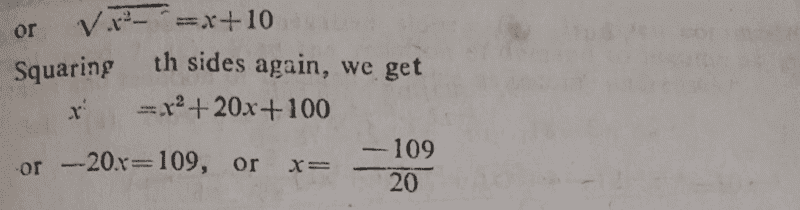
This is well understood. I was trying to look at the problem from a different perspective. (see attached below my attempt);
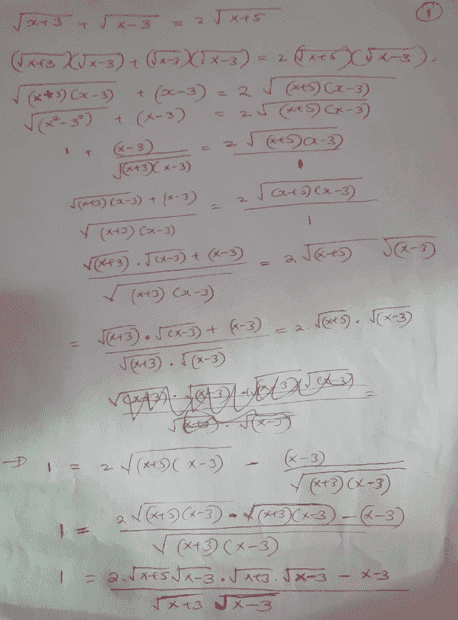
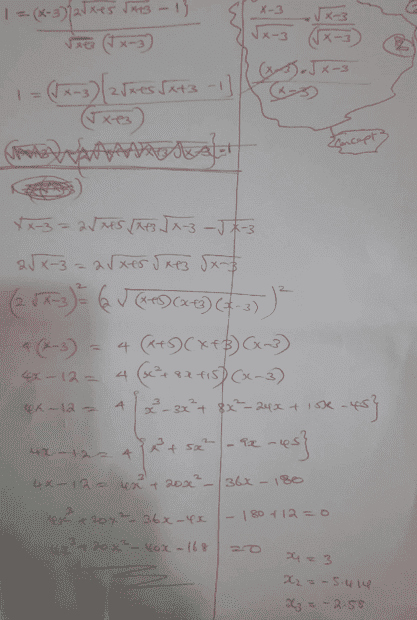
Makes any sense? cheers...
ok i can see some mistake...i will amend it later...let me amend it first then you guys can chime in later..
...I seem to be going round in circles...looks like squaring both sides would realize what we want...
This is well understood. I was trying to look at the problem from a different perspective. (see attached below my attempt);
Makes any sense? cheers...
ok i can see some mistake...i will amend it later...let me amend it first then you guys can chime in later..
...I seem to be going round in circles...looks like squaring both sides would realize what we want...
Last edited: