Solve for ##x## involving modulus

[brotherbobby]

Homework Statement

Solve $|x|+|x-2|=2$

Relevant Equations

1. For a given function $f(x)$, if $|f(x)|<a \Rightarrow -a < f(x) < a$
2. For a given function $f(x)$, if $|f(x)|>a\Rightarrow f(x)<-a\; \text{or}\; f(x)>a$

(I could solve the problem but could not make sense of the solution given in the text. Let me put my own solutions below first).

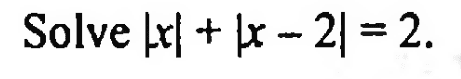1. Problem Statement : I copy and paste the problem to the right as it appears in the text.

2. My attempt : There are three "regions" where $x$ can lie.

(1) $\mathbf{x \ge 2}$ : In this case we have given $|x|+|x-2|=2\Rightarrow x+x-2 = 2\Rightarrow 2x=4\Rightarrow \boxed{x=2}$ (as the answer $x=2$ lies within the selected range in which the equation is solved).

(2) $\mathbf{0\le x<2}$ : For this case, the equation: $|x|+|x-2|=2\Rightarrow x+2-x = 2 \Rightarrow 2=2$ which is always true. Hence the selected range is a solution : $\boxed{0\le x<2}$.

(3) $\mathbf{x<0}$ : In this case, the given equation : $|x|+|x-2|=2\Rightarrow -x+2-x = 2\Rightarrow 2x=0\Rightarrow x=0$. This solution has to be rejected for it doesn't lie in the selected range.

Hence, the solution to the problem : $\boxed{0\le x\le 2}$. $\Large{\checkmark}$, as it agrees with the answer in the text.

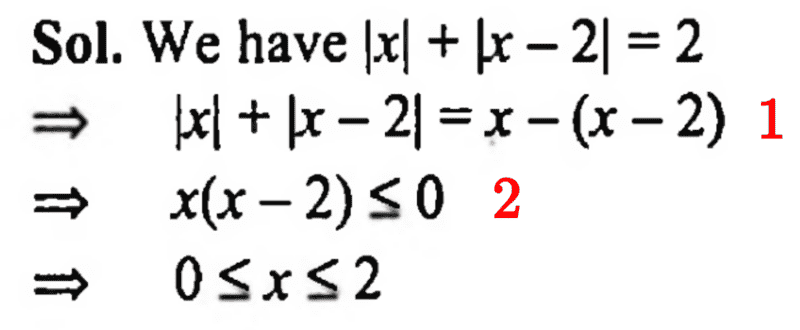3. The text's attempt : I copy and paste the solution in the text given to the right.

It is the solution that I am struggling to follow. Namely on the two steps marked as 1 and 2.

In 1, the author is tacitly assuming that $x>0$ and that $x<2$. What is the reason for this assumption? There are three broad regions where $x$ can lie, as I have shown in my solution above. Why take the one on the middle, as he has done?

2 is more confusing. How can the expression $x-(x-2)=2$ become $x(x-2)\le 0$?

A hint or suggestion referring to the author's solution would be welcome. I admit that he obtains the same answer as I do.

 

[PeroK]

I wouldn't particularly worry about the text solution as yours is better.

Note that the one-way implication given in the text is not enough. It needs two-way implication.

 

[PeroK]

Re your first question, the author has replaced the $2$ on the RHS by the equivalent $x - (x -2)$.

 

[Delta2]

@PeroK said how (1) result. For the (2), just square both sides of (1). After simplifications you ll get $$|x||x-2|=-x(x-2)\iff |x(x-2)|=-x(x-2)$$

 

[brotherbobby]

Re your first question, the author has replaced the $2$ on the RHS by the equivalent $x - (x -2)$.

Ahh how silly of me. Yes indeed $2 = x-(x-2)$, as an identity, independent of the problem. The author's solution not only makes sense but is superior to my own. Let me explain.

But first, I forgot to mention something in the Relevant Equations. That $|x|+|y| = |x-y|$, if $x$ and $y$ are of opposite signs. Or one of them can be zero.

Attempt :
\begin{equation*}
\begin{split}
|x|+|x-2|&=2\\
& = |2|\\
&=|x-(x-2)|\\
\Rightarrow x(x-2)&\le 0 \mathbf{*}\\
&\Rightarrow\boxed{0\le x \le 2}
\end{split}
\end{equation*}

* Since the line above implies that (x) and (x-2) must be of opposite signs, referring to my Relevant Equations.

 

[PeroK]

A simple approach is to draw a graph of the function $|x| + |x-a|$ and note that it has a constant value of $a$ in the interval $[0,a]$ and linear on either side.

That also solves the more general problem of $|x| + |x-a| = b$.

 

[Delta2]

A simple approach is to draw a graph of the function $|x| + |x-a|$ and note that it has a constant value of $a$ in the interval $[0,a]$ and linear on either side.

That also solves the more general problem of $|x| + |x-a| = b$.

ehm was that a typo you meant to write the more general problem $|x|+|x-a|=a$?

 

[PeroK]

ehm was that a typo you meant to write the more general problem $|x|+|x-a|=a$?

No, the general case where $a \ne b$.

 

[Delta2]

No, the general case where $a \ne b$.

Hmm, if $b\neq a$ then it has at most two solutions right? Not an interval of solutions.

 

[PeroK]

Hmm, if $b\neq a$ then it has at most two solutions right? Not an interval of solutions.

Yes. My point was really if we draw a graph of the function, then all is clear.

 

[nuuskur]

It is necessary that the solutions lie in said interval. Conversely, given any $x\in [0,2]$ one readily verifies it satisfies the equality.