arildno
Science Advisor
Homework Helper
Gold Member
Dearly Missed
- 10,135
- 138
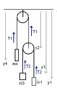
Hmm..seems I specified 4 equations, rather than 3.
The kinematic relation between the two accelerations is the one that is lacking; it represents a distinct constraint requirement the rest does not provide for (and which is embedded in the Lagrangian equations of motion).
The kinematic relation between the two accelerations is the one that is lacking; it represents a distinct constraint requirement the rest does not provide for (and which is embedded in the Lagrangian equations of motion).