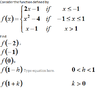Solve Multiline Function w/2 Variables - Explanation Here

  • Context: MHB 
  • Thread starter Thread starter tobiajj1
  • Start date Start date
  • Tags Tags
    Functions
Click For Summary
SUMMARY

This discussion focuses on solving a multiline function with two variables, specifically examining the function f(1 - h) where 0 < h < 1. Participants clarify that this implies 0 < x < 1, leading to the question of determining f(x). The expression h^2 - 2h - 3 is introduced as part of the problem-solving process. The conversation emphasizes the need for a clear understanding of the function's behavior within the specified range.

PREREQUISITES
  • Understanding of multiline functions
  • Knowledge of variable constraints in mathematical functions
  • Familiarity with function notation and evaluation
  • Basic algebra skills, particularly polynomial expressions
NEXT STEPS
  • Explore the properties of multiline functions in calculus
  • Study the implications of variable constraints on function behavior
  • Learn about polynomial function analysis and graphing
  • Investigate advanced function types, such as piecewise functions
USEFUL FOR

Mathematicians, students studying calculus, and anyone interested in understanding the behavior of multiline functions with variable constraints.

tobiajj1
Messages
2
Reaction score
0
Can anyone explain how to solve a multiline function with two variables? Please see attached.
 

Attachments

  • multiline Function.png
    multiline Function.png
    5.1 KB · Views: 88
Physics news on Phys.org
tobiajj1 said:
Can anyone explain how to solve a multiline function with two variables? Please see attached.
If you are referring to f(1 - h), for example, You know that 0 < h < 1, so you know that 0 < 1 - h < 1 and thus 0 < x < 1. What is f(x)?

-Dan
 
h^2-2h-3?
topsquark said:
If you are referring to f(1 - h), for example, You know that 0 < h < 1, so you know that 0 < 1 - h < 1 and thus 0 < x < 1. What is f(x)?

-Dan
 
tobiajj1 said:
h^2-2h-3?
That's it! What about the other one?

-Dan
 

Similar threads

Undergrad Question on Lambert W function
  • · Replies 27 ·
Replies
27
Views
5K
Undergrad Multivariable function optimization inconsistency
  • · Replies 3 ·
Replies
3
Views
2K
MHB Finding minimum value of function with two variable
  • · Replies 7 ·
Replies
7
Views
3K
Undergrad How to manipulate functions that are not explicitly given?
  • · Replies 16 ·
Replies
16
Views
3K
Undergrad What Are Common Misconceptions About the Dirac Delta Function?
  • · Replies 25 ·
Replies
25
Views
4K
High School How do I invert this exponential function?
  • · Replies 3 ·
Replies
3
Views
4K
MHB Increase and decrease functions
  • · Replies 1 ·
Replies
1
Views
2K
MHB Prove that dirichlet function is periodic
  • · Replies 6 ·
Replies
6
Views
4K
MHB How to use change of variables technique here?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Write function to model combined rate
  • · Replies 1 ·
Replies
1
Views
1K