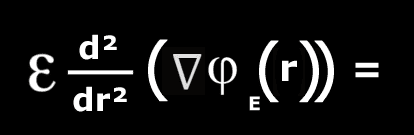Discussion Overview
The discussion revolves around an equation that participants are trying to contextualize, particularly focusing on the contents of the brackets within it. The conversation explores potential applications, interpretations, and the nature of the equation itself, touching on concepts from physics and mathematics.
Discussion Character
- Exploratory
- Debate/contested
- Technical explanation
- Mathematical reasoning
Main Points Raised
- Some participants suggest that the equation may relate to mathematical problems, particularly involving derivatives, with a focus on the third derivative with respect to ##r##.
- One participant proposes that ##\phi_E## could represent the scalar potential of the electric field, linking it to the electric field equation in electrostatics.
- Several participants emphasize that the expression in question is not a complete equation, as it lacks a right-hand side, leading to various interpretations of its meaning.
- One participant speculates that assuming the right-hand side is zero could lead to interpretations related to wave equations in the context of electric fields.
- Another participant raises concerns about the necessity of formulating equations in terms of covariant objects for vector fields, questioning the clarity of the right-hand side.
- Discussion includes references to the d'Alembertian operator and its relation to the Laplacian, with some participants seeking clarification on covariant versus contravariant notation.
- One participant notes the lack of engagement from the original poster, suggesting that the inquiry may not be actively pursued.
Areas of Agreement / Disagreement
Participants express differing views on the nature of the equation and its components, with no consensus reached regarding its interpretation or the implications of the right-hand side. The discussion remains unresolved with multiple competing interpretations.
Contextual Notes
Participants highlight the ambiguity surrounding the right-hand side of the equation and the need for clarity in formulating equations involving vector fields. There are also references to specific mathematical notations that may not be universally understood among participants.
Who May Find This Useful
This discussion may be of interest to those exploring mathematical physics, particularly in the context of electric fields, wave equations, and the nuances of mathematical notation in physics.