Solve Pressure at X & Y in Manometer Problem

[MrMechanic]

Homework Statement

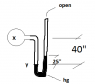
A simple mercury manometer connected into a flow line gives readings as shown in the figure. Local gravity is standard and the mercury density is 0.488lb/in^3. Find the pressure at points X and Y when the flow line and left leg contain (a) air whose density is 0.072lb/ft^3, (b) water whose density is 62.1lb/ft^3. (c) Answer (a) and (b) if the local gravity is g= 30ft/s^2.


ANSWER: (a) 26.90, 26.90, (b) 25.46, 26.90, (c) 26.10 psia

Homework Equations

Pressure = pgh

The Attempt at a Solution

I've done getting Py but I can't find Py at (a)
Also I've tried solving (b) but i can't solve it actually.
Here's my solution on Py at (a)
Py = 14.7psi + (0.072lb/ft^3 / 12^3 in^3)(15) + (0.488lb/in^3)(25) =26.90psi

 

[Chestermiller]

Your equation for py at (a) for the left column filled with air is incorrect. The "air term" should not be there. If the left column is filled with water, the corresponding "water term" should not be there either. The air and water columns only come in when you are trying to get the pressure at point x...and then they should be subtracted.

Chet

 

[MrMechanic]

Thanks for replying. The left column is filled water. While the right column is filled with air?
Do you mean that I should use Py = 14.7psi + 0.488(25) = 26.9
then how about Px?

 

[MrMechanic]

I'm thinking and re-reading the problem stated above. I just noticed this "Find the pressure at points X and Y WHEN THE FLOW LINE AND THE LEFT LEG CONTAIN" So does that mean ...The left leg & the right leg contain a specific condition each letter (a and b) right?

 

[Chestermiller]

Thanks for replying. The left column is filled water. While the right column is filled with air?

The left column is filled with either air or water above the Hg. The right colunm is filled with air above the mercury.

Do you mean that I should use Py = 14.7psi + 0.488(25) = 26.9

Yes.

then how about Px?

For (a), Px=Py-(0.072lb/ft^3 / 12^3 in^3)(15)
For (b), Px=Py-(62.1lb/ft^3 / 12^3 in^3)(15)

Chet

 

[MrMechanic]

And I don't really know what a flow line is...

 

[Chestermiller]

And I don't really know what a flow line is...

I think that circle with the x inside it represents a pipe running into the paper. Water or air is flowing through that pipe.

Chet

 

[MrMechanic]

I see. Wow. Now I know what you mean when you said that my Py is incorrect. Thanks.
and for (b) i don't really know where did they put the water. So I'm totally confused. I'm done with (a). Thanks for helping Sir Chet!

 

[MrMechanic]

(a)
Py=14.7psi + 0.488(25) = 26.9
Px=26.9-(0.072lb/ft^3 / 12^3 in^3)(15) =26.9

(b)
Py = 14.7 + (62.1/12^3)(15) + (0.488x25)?? <--- not really sure about this.

 

[MrMechanic]

at (b) i think i got Px but I'm not really sure about it.
Px = Py - (62.1/12^3 x 40) =25.46

I got Py using what we did above.

 

[Chestermiller]

at (b) i think i got Px but I'm not really sure about it.
Px = Py - (62.1/12^3 x 40) =25.46

I got Py using what we did above.

Yes. It isn't clear from the diagram whether it should be a 40 or a 15. Visually, if the diagram is close to scale, the 40 is the correct number to use.

Chet

 

[MrMechanic]

Thanks for clearing that up! Could you explain to me what should I do on (c). (a) and (b) if the local gravity is g= 30ft/s^2. I haven't use the local gravity yet...

 

[Chestermiller]

Thanks for clearing that up! Could you explain to me what should I do on (c). (a) and (b) if the local gravity is g= 30ft/s^2. I haven't use the local gravity yet...

Well, normal gravity is 32.2 ft/sec^2. From your equations for the hydrostatic pressure variation, how would the hydrostatic contributions change if g were only 30? Have you learned how to work with the "american" system of units, and with using g_c=32.2?

Chet

 

[MrMechanic]

Yes sir. But I couldn't find a way to start using the equations that I learned from my Professor.

 

[MrMechanic]

How would I start (c) ... If the gravity changed to 30ft/sec^2 then what would be the starting equation to get 26.10psia.

 

[Chestermiller]

In the units you are using, ΔP=ρ\frac{g}{g_c}h, where ΔP is in lb_force/in², ρ is the density in lb_mass/in^3, g is the local acceleration of gravity (ft/sec²), h is the height of the column in inches, and g_c is the constant 32.2 \frac{lb_{mass}ft}{lb_{force}sec^2}.

Chet

 

[MrMechanic]

Hmmm. Let me know if this is the correct equation sir...
P = (0.072) x (30/32.2) (40/12)
when i get that should I make another equation for Water?
P = (62.1) x (30/32.2) (40/12)
and sum what I got? is it the correct procedure?
Since,
Pabs = Patm + Pgage i think.

 

[Chestermiller]

Hmmm. Let me know if this is the correct equation sir...
P = (0.072) x (30/32.2) (40/12)
when i get that should I make another equation for Water?
P = (62.1) x (30/32.2) (40/12)
and sum what I got? is it the correct procedure?
Since,
Pabs = Patm + Pgage i think.

Don't forget to also do this for the Hg.

Chet

 

[MrMechanic]

Pabs = Pair + PH20 + PHg + Patm?

So i got this...

Pair = 0.02lb/ft^3 /12^3 x (30/32.2) (40) = 1/644 psi
PH20 = 62.1 / 12^3 x (30/32.2)(40)= 1.339psi
PHg = 0.488 x (30/32) (40) = 18.19psi

Is it wrong?

 

[MrMechanic]

Well, I kinda worked out the formula you gave me.
So, here is my solution to (c) ΔP=(0.488)(30/32.2)x(25) = 11.38 lb/in^2
Pgage = 11.38
Pabs = Patm + Pgage
Pabs = 14.7 + 11.38
Pabs = 26.08 psia

 

[Chestermiller]

Well, I kinda worked out the formula you gave me.
So, here is my solution to (c) ΔP=(0.488)(30/32.2)x(25) = 11.38 lb/in^2
Pgage = 11.38
Pabs = Patm + Pgage
Pabs = 14.7 + 11.38
Pabs = 26.08 psia

Good job.

Chet