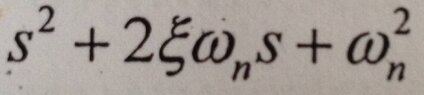Discussion Overview
The discussion revolves around solving a quadratic equation presented in a somewhat unconventional format, specifically involving the Greek letter 'E' (xi) and its implications in the equation. Participants explore methods to approach the solution, including the use of the quadratic formula, while expressing varying levels of understanding and frustration with the complexity of the problem.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Homework-related
- Mathematical reasoning
Main Points Raised
- One participant expresses confusion about the quadratic equation due to the presence of the Greek letter 'E', suggesting it complicates their understanding.
- Another participant proposes that 'E' should be treated as a constant, similar to a numerical value.
- There is a suggestion to use the quadratic formula with identified coefficients a = 1, b = 2ξω_n, and c = ω_n².
- Participants discuss the formatting of mathematical symbols and share tips on how to write them correctly in the forum.
- One participant expresses frustration about the lack of prior exposure to the quadratic formula, feeling unprepared for the assignment.
- Another participant acknowledges the algebraic mistakes made in the calculations and suggests reviewing foundational concepts.
- There is a discussion about the derivation of the quadratic formula and the importance of understanding the underlying principles of quadratic equations.
- A participant shares an update about receiving incorrect materials from their tutor, which contributed to their confusion.
Areas of Agreement / Disagreement
Participants express a range of views on how to approach the problem, with some agreeing on the use of the quadratic formula while others remain uncertain about the calculations. There is no consensus on the best method to solve the equation, and several participants highlight their struggles with the material.
Contextual Notes
Participants note that the problem may be unreasonable given the limited prior exposure to the quadratic formula, which typically requires a more comprehensive understanding of quadratic equations, including factoring and completing the square.
Who May Find This Useful
This discussion may be useful for students encountering quadratic equations for the first time, particularly those struggling with the transition from simpler factoring methods to more complex applications involving the quadratic formula.