Solve the given problem involving probability without replacement

[chwala]

Homework Statement

This is apast paper question. Allow me to post it as it is.

Relevant Equations

Probability

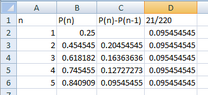
Okay, i was able to solve it by trial and error, i am seeking for a more concrete approach. Can combination work here? or a more solid approach using sequences? or probability itself?

My trial and error,
$P_{green} = \dfrac{9}{12}×\dfrac{8}{11} ×\dfrac{7}{10}×\dfrac{6}{9}×\dfrac{3}{8} = \dfrac{21}{220}$

$n=5$.

and why 2 marks? or there is a shorter method.

 

[phinds]

and why 2 marks?

And how should we know how many marks there are supposed to be? Is 2 not a perfect score for this question?

 

[Hill]

a more concrete approach

Excel:

The calculated value in C6 equals the target value in D6 when n=5.