Solve the problem involving probability density function

[chwala]

Homework Statement

see attached

Relevant Equations

Statistics

This is the question:

This is the ms solution- from Further Maths paper.

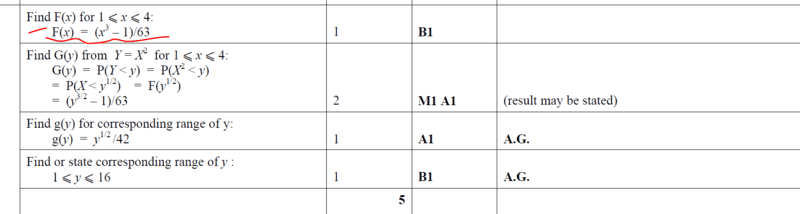My question is referenced to the highlighted part. I can see they substituted for the lower limit i.e $x=1$ to get: $F(x)=\dfrac{x^3-1}{63}$
supposing our limits were; $2≤x≤4$ would the same approach apply? Anything wrong if we substitute the upper limit i.e $x=4$? and have our:
$F(x)=\dfrac{64-x^3}{63}?$

 

[pasmith]

I don't understand your question.

If $f$ is to be a PDF for a random variable $X$ taking values in $[a,b]$ we must have $$\int_a^b f(x)\,dx = 1.$$ If that is the case, then for $a \leq c < d \leq b$ we have $$P(c \leq X \leq d) = \int_c^d f(x)\,dx.$$

 

[chwala]

I don't understand your question.

If $f$ is to be a PDF for a random variable $X$ taking values in $[a,b]$ we must have $$\int_a^b f(x)\,dx = 1.$$ If that is the case, then for $a \leq c < d \leq b$ we have $$P(c \leq X \leq d) = \int_c^d f(x)\,dx.$$

That's clear...my question is suppose we substitute the upper limit ; $x=4$ instead of lower limit; $x=1$ to get $F(x)$, would that be correct? Note that when we integrate $f(x)$, we shall get the indefinite integral,$F(x)$= $\dfrac{x^3}{63}$.

 

[pasmith]

By definition, $$F(x) = P(X \leq x) = \int_1^x f(x)\,dx.$$ Not integrating from 1 to $x$ will not give you $F(x)$.

 

[chwala]

By definition, $$F(x) = P(X \leq x) = \int_1^x f(x)\,dx.$$ Not integrating from 1 to $x$ will not give you $F(x)$.

Noted thanks @pasmith. Let me look at this again. The concept is clear, was just wondering if we could reverse the order but that does not seem to work going with the general definition of probability density function.

 

[chwala]

What of: $$-\int_x^1 f(x)dx=\int_1^x f(x)dx?$$ in our case
$$-\int_ x^1 \left[\dfrac{x^2}{21}\right] dx=-\int_ 4^x \left[\dfrac{x^2}{21}\right] dx=-\left[\dfrac{x^3-64}{63}\right]?$$

 

[Office_Shredder]

You're missing a 1- when you switch the bound from 1 to 4 since you're computing the complement probability.

 

[chwala]

You're missing a 1- when you switch the bound from 1 to 4 since you're computing the complement probability.

I am not getting you...what I wanted to know is, "will my $F(x)$ in post $6$ be correct?' Having changed the bounds...

 

[Office_Shredder]

No. The last line starts by saying $P(X < x) = P(X> x)$. It's not though, you should use $P(X < x) =1- P(X> x)$

You can verify you got the wrong answer by seeing that for you, $F(1)\neq 0$