docnet
- 796
- 486
- Homework Statement
- solve this PDE
- Relevant Equations
- $$\tilde{u}(t,x)=\frac{1}{2}\Big[\tilde{g}(x+t)+\tilde{g}(x-t)\Big]+\frac{1}{2}\int^{x+t}_{x-t}\tilde{h}(y)dy$$
Hi all, I was hoping someone could check whether I computed part (4) correctly, where i find the solution u(t,x) using dAlembert's formula:
$$\boxed{\tilde{u}(t,x)=\frac{1}{2}\Big[\tilde{g}(x+t)+\tilde{g}(x-t)\Big]+\frac{1}{2}\int^{x+t}_{x-t}\tilde{h}(y)dy}$$
Does the graph of the solution look correct or does it look off?
I posted all my work just in case someone feels like looking over them ;)


We consider for an unknown function ##u:[0,\infty)\times[0,\infty)\rightarrow \mathbb{R}## the Neumann initial value problem given by
$$
\begin{cases}
\partial_t^2u-\partial_x^2u=0 & \text{in}\quad (0,\infty)\times (0,\infty) \\
u=g & \text{on}\quad\{t=0\}\times(0,\infty)\\\partial_tu=h & \text{on}\quad \{t=0\}\times (0,\infty) \\
\partial_xu=0 & \text{on}\quad (0,\infty)\times\{x=0\}\end{cases}$$
(1) Use even extension in the spatial variable ##x## to extend the unknown function ##u## and the data ##g,h## to functions ##\tilde{u}:[0,\infty)\times \mathbb{R}\rightarrow \mathbb{R}## and ##\tilde{g},\tilde{h}:\mathbb{R}\rightarrow \mathbb{R}##. \\\\We define the even extended functions with the following piece-wise functions
$$\tilde{u}(t,x)=
\begin{cases}
u(t,x) & t\geq 0, x\geq0 \\
u(t,-x) & t\geq 0, x<0
\end{cases}$$$$\ \tilde{g}(x)=
\begin{cases}
g(x) & x\geq0 \\
g(-x) & x<0
\end{cases}$$
$$\tilde{h}(x)=
\begin{cases}
h(x) & x\geq0 \\
h(-x) & x<0
\end{cases}$$
(2) The initial value problem satisfied by the unknown function ##\tilde{u}## with data ##\tilde{g}## and ##\tilde{h}## is
$$\begin{cases}
\partial_t^2\tilde{u}-\partial_x^2\tilde{u}=0 & \text{in}\quad (0,\infty)\times \mathbb{R} \\
\tilde{u}(0,\cdot)=\tilde{g} & \text{on}\quad\{t=0\}\times\mathbb{R}\\\partial_t\tilde{u}(0,\cdot)=\tilde{h} & \text{on}\quad \{t=0\}\times\mathbb{R} \end{cases}$$
The first equation is true because for ##x<0##
$$\partial_t^2u(t,x)\Rightarrow \partial_t^2u(t,-x)$$
$$\partial_x^2u(t,x)\Rightarrow \partial_x^2u(t,-x)$$
(3) We solve this problem by
plugging in ##u_0=\tilde{g}## and ##u_1=\tilde{h}## into d'Alembert's formula
$$\boxed{\tilde{u}(t,x)=\frac{1}{2}\Big[\tilde{g}(x+t)+\tilde{g}(x-t)\Big]+\frac{1}{2}\int^{x+t}_{x-t}\tilde{h}(y)dy}$$
(4) To recover ##u## from ##\tilde{u}##, We consider the solution formula for the following two cases: ##0\leq t\leq x## and
##0\leq x\leq t##.
Let ##t\geq 0, x\geq 0##.
$$1. \quad x+t\geq 0 \Rightarrow \tilde{g}(x+t)=g(x+t)$$
$$2. \quad x-t \Rightarrow x-t\geq 0 \quad \text{or} \quad x-t<0$$
If $x-t\geq 0$ $$\tilde{g}(x-t)\Rightarrow(x-t)$$
$$\int^{x+t}_{x-t}\tilde{h}(y)dy\Rightarrow \int^{x+t}_{x-t}h(y)dy$$
If ##x-t<0##
$$\tilde{g}(x-t)=g(t-x)$$
$$\int^{x+t}_{x-t}\tilde{h}(y)dy\Rightarrow \int_{t-x}^{x+t}h(y)dy$$
Hence our solution is given by
$$u(t,x)=\frac{1}{2}\Big[g(x+t)+g(x-t)\Big]+\frac{1}{2}\int^{x+t}_{x-t}h(y)dy \quad \text{for} \quad 0\leq t \leq x $$ $$
u(t,x)=\frac{1}{2}\Big[g(x+t)+g(t-x)\Big]+\frac{1}{2}\int_{t-x}^{x+t}h(y)dy \quad \text{for} \quad 0\leq x \leq t$$
(5) We choose ##g(x)=x^2## and ##h(y)=y## then the solution is given by
$$u(t,x)=x^2+t^2+xt\quad \text{for} \quad 0\leq t \leq x \quad \text{and} \quad 0\leq x \leq t$$
Sketch of the solution for ##t=0,1,2,3##
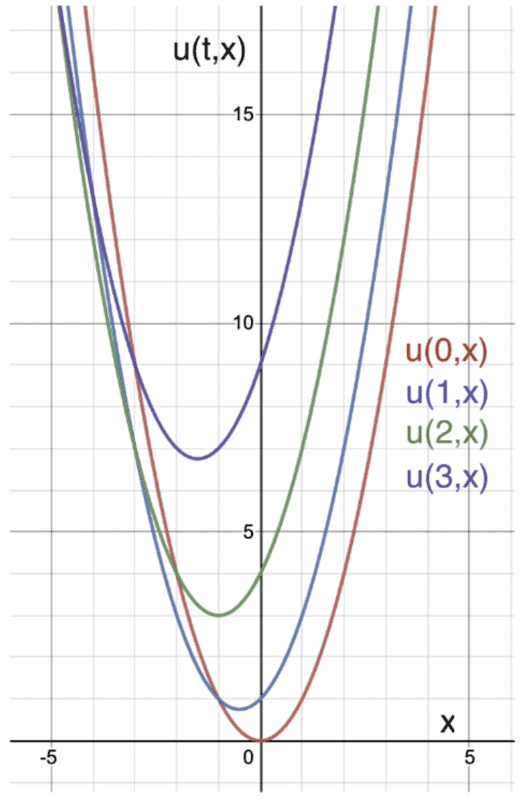
$$\boxed{\tilde{u}(t,x)=\frac{1}{2}\Big[\tilde{g}(x+t)+\tilde{g}(x-t)\Big]+\frac{1}{2}\int^{x+t}_{x-t}\tilde{h}(y)dy}$$
Does the graph of the solution look correct or does it look off?
I posted all my work just in case someone feels like looking over them ;)
We consider for an unknown function ##u:[0,\infty)\times[0,\infty)\rightarrow \mathbb{R}## the Neumann initial value problem given by
$$
\begin{cases}
\partial_t^2u-\partial_x^2u=0 & \text{in}\quad (0,\infty)\times (0,\infty) \\
u=g & \text{on}\quad\{t=0\}\times(0,\infty)\\\partial_tu=h & \text{on}\quad \{t=0\}\times (0,\infty) \\
\partial_xu=0 & \text{on}\quad (0,\infty)\times\{x=0\}\end{cases}$$
(1) Use even extension in the spatial variable ##x## to extend the unknown function ##u## and the data ##g,h## to functions ##\tilde{u}:[0,\infty)\times \mathbb{R}\rightarrow \mathbb{R}## and ##\tilde{g},\tilde{h}:\mathbb{R}\rightarrow \mathbb{R}##. \\\\We define the even extended functions with the following piece-wise functions
$$\tilde{u}(t,x)=
\begin{cases}
u(t,x) & t\geq 0, x\geq0 \\
u(t,-x) & t\geq 0, x<0
\end{cases}$$$$\ \tilde{g}(x)=
\begin{cases}
g(x) & x\geq0 \\
g(-x) & x<0
\end{cases}$$
$$\tilde{h}(x)=
\begin{cases}
h(x) & x\geq0 \\
h(-x) & x<0
\end{cases}$$
(2) The initial value problem satisfied by the unknown function ##\tilde{u}## with data ##\tilde{g}## and ##\tilde{h}## is
$$\begin{cases}
\partial_t^2\tilde{u}-\partial_x^2\tilde{u}=0 & \text{in}\quad (0,\infty)\times \mathbb{R} \\
\tilde{u}(0,\cdot)=\tilde{g} & \text{on}\quad\{t=0\}\times\mathbb{R}\\\partial_t\tilde{u}(0,\cdot)=\tilde{h} & \text{on}\quad \{t=0\}\times\mathbb{R} \end{cases}$$
The first equation is true because for ##x<0##
$$\partial_t^2u(t,x)\Rightarrow \partial_t^2u(t,-x)$$
$$\partial_x^2u(t,x)\Rightarrow \partial_x^2u(t,-x)$$
(3) We solve this problem by
plugging in ##u_0=\tilde{g}## and ##u_1=\tilde{h}## into d'Alembert's formula
$$\boxed{\tilde{u}(t,x)=\frac{1}{2}\Big[\tilde{g}(x+t)+\tilde{g}(x-t)\Big]+\frac{1}{2}\int^{x+t}_{x-t}\tilde{h}(y)dy}$$
(4) To recover ##u## from ##\tilde{u}##, We consider the solution formula for the following two cases: ##0\leq t\leq x## and
##0\leq x\leq t##.
Let ##t\geq 0, x\geq 0##.
$$1. \quad x+t\geq 0 \Rightarrow \tilde{g}(x+t)=g(x+t)$$
$$2. \quad x-t \Rightarrow x-t\geq 0 \quad \text{or} \quad x-t<0$$
If $x-t\geq 0$ $$\tilde{g}(x-t)\Rightarrow(x-t)$$
$$\int^{x+t}_{x-t}\tilde{h}(y)dy\Rightarrow \int^{x+t}_{x-t}h(y)dy$$
If ##x-t<0##
$$\tilde{g}(x-t)=g(t-x)$$
$$\int^{x+t}_{x-t}\tilde{h}(y)dy\Rightarrow \int_{t-x}^{x+t}h(y)dy$$
Hence our solution is given by
$$u(t,x)=\frac{1}{2}\Big[g(x+t)+g(x-t)\Big]+\frac{1}{2}\int^{x+t}_{x-t}h(y)dy \quad \text{for} \quad 0\leq t \leq x $$ $$
u(t,x)=\frac{1}{2}\Big[g(x+t)+g(t-x)\Big]+\frac{1}{2}\int_{t-x}^{x+t}h(y)dy \quad \text{for} \quad 0\leq x \leq t$$
(5) We choose ##g(x)=x^2## and ##h(y)=y## then the solution is given by
$$u(t,x)=x^2+t^2+xt\quad \text{for} \quad 0\leq t \leq x \quad \text{and} \quad 0\leq x \leq t$$
Sketch of the solution for ##t=0,1,2,3##
