Solve Urgently Needed: Related Rates Swimming Pool Problem

[rum2563]

Homework Statement

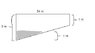
A swimming pool is 24 m long by 8 m wide, 1 m deep at the shallow end and 3 m deep at the deep end, the bottom being an inclined plane. If water is pumped into the empty pool at a rate of 2m^3/min, then how fast is the water level rising at the moment when the water is 1 m deep at the end of the pool.

Homework Equations

dh/dt = 1/As x dV/dt

As: area of exposed surface

The Attempt at a Solution

Basically I used ratios to get the length of the pool when the height is 1 m deep.

1/3 = x/24
So x = 8 m.

Then As = 8*8 = 64 m^2

dh/dt = 2/64
= 1/32 m/min

I am not sure what I am doing wrong. I have my diagram attached. Please tell me what I am doing wrong. Also, if you have the answer please tell me because I need this urgently. I can use the answer and then work it back to get everything right.

Thanks.

 

[Dick]

The surface area 'As' is a function of time as well, it's not just a constant you can factor out.

 

[rum2563]

So would that I mean I have to use some other formula rather than the As one. Because my teacher told me that formula is good for any questions which have exposed area.

 

[Dick]

Volume(t)=(1/2)*As(t)*h(t) since the volume is 1/2 of a rectangular solid. So you have to use the product rule to get dV/dt. Your teacher may have exaggerated the usefulness of "dh/dt = 1/As x dV/dt". That's only good if As is a constant.

 

[rum2563]

Um, I am sorry I cannot understand. Perhaps if you could explain without As because it's confusing to me.
Please. Thanks.

 

[Dick]

Good idea. Write a formula for the volume of the pool without using As. V=(1/2)*h*(8m)*(h*24/3). h*24/3 is the length of the filled part. I got that from you 1/3=x/24 by replacing 1 with h. Now how is dV/dt related to dh/dt? Notice As=(8m)*(h*24/3).

 

[rum2563]

sorry for the late reply.
I am extremely confused.

How did you get the formula for the volume of pool? Also, I understand that as the height increases, the volume increases too.

Exposed surface will be a rectangle, so area would be length by width.
I understand the width is 8 m and the length is (24h)/3.

But if we solve the volume formula you gave, we end up with the same conclusion that dh/dt is 1/32 m/min.

Please do explain. I really need to know how this works. Thanks.

 

[Dick]

I got the formula by multiplying the area of the triangular cross section of the pool by the width. Yes, you get the same answer of 1/32 m/min. Because that's the correct answer. There is also nothing wrong with dV/dt=(1/As)*dh/dt. You seemed to be so convinced you were wrong that you convinced me. Why do you think 1/32 m/min is wrong?

 

[rum2563]

I got the formula by multiplying the area of the triangular cross section of the pool by the width. Yes, you get the same answer of 1/32 m/min. Because that's the correct answer. There is also nothing wrong with dV/dt=(1/As)*dh/dt. You seemed to be so convinced you were wrong that you convinced me. Why do you think 1/32 m/min is wrong?

LOL.The reason why I think it's wrong is because my teacher did not give me marks for the answer 1/32 m/min. That is why I think there must be some twist to it.

And when I showed my calculations for h/3 = x/24 the teacher also put a "x" mark there.


Maybe then I did it right, I am not sure.

 

[Dick]

LOL.The reason why I think it's wrong is because my teacher did not give me marks for the answer 1/32 m/min. That is why I think there must be some twist to it.

And when I showed my calculations for h/3 = x/24 the teacher also put a "x" mark there.


Maybe then I did it right, I am not sure.

Well, I think you did it right.

 

[jimvoit]

Here is a solution that I present only because you say the (1/32) solution didn’t go well with your instructor. My math, being what it is, I would treat it with suspicion.

Let b be the length of the surface of the water in the 24 meter direction.
Let h be the depth of the water at the deep end of the pool.
Let v be the volume of water in the pool at time t.

b = 12 h
v = (1/2) h (12 h) 8 = 48 h^2
dv/dt = 96 h dh/dt
dh/dt = 1/(96 h) dv/dt

At h = 1 and dv/dt = 2
dh/dt = 1/(96×1)×2 = 1/48

 

[Dick]

Here is a solution that I present only because you say the (1/32) solution didn’t go well with your instructor. My math, being what it is, I would treat it with suspicion.

Let b be the length of the surface of the water in the 24 meter direction.
Let h be the depth of the water at the deep end of the pool.
Let v be the volume of water in the pool at time t.

b = 12 h
v = (1/2) h (12 h) 8 = 48 h^2
dv/dt = 96 h dh/dt
dh/dt = 1/(96 h) dv/dt

At h = 1 and dv/dt = 2
dh/dt = 1/(96×1)×2 = 1/48

That would be fine, except I question the b=12h. At h=0, b=0. At h=3, b=24. So b=8h.

 

[jimvoit]

The bottom of the pool terminates at the shallow end at h=2, not h=3. At h=2, b=24.

 

[Dick]

Oooooooops. You've got it. I was looking at the attached JPG and reading the little tick mark near the 3m label as the depth of the slanted section. Silly me. Sorry. Thanks!

 

[rum2563]

Thanks jimvoit. I finally get it. Your answer was very detailed and it helped me understand this question. The answer 1/48 seems better than the one I got, also the fact that it is 2m and not 3m for the ratios was a small mistake that I had made, but your post was really helpful.
You are the best.
Thanks again.

 

[jimvoit]

I’m glad we were able to help out. If there is a lesson here, it is that things can go wrong in at least 2 ways…First if the translation from the description of the physical situation to the math is faulted, and second if the math is faulted. The first way is a real headache because perfectly good math can lead to the wrong answer.

 

[Dick]

You can also go wrong by focusing on the big picture and forgetting to check the little details. As we did. Thanks again.