Solving a differential equation using Laplace transform

[PainterGuy]

TL;DR

What is the criteria for a given differential equation to be solvable using Laplace transform?

Hi,

I was trying to see if the following differential equation could be solved using Laplace transform; its solution is y=x^4/16.

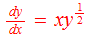
You can see below that I'm not able to proceed because I don't know the Laplace pair of xy^(1/2).

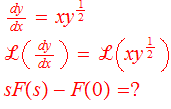
Is it possible to solve the above equation using Laplace transform? In my opinion, I don't think so.

Thank you.

 

[S.G. Janssens]

Your ODE is nonlinear in the unknown $y$.

 

[pasmith]

In this case, the substitution $u = y^{1/2}$ will reduce the ODE to one which can be solved by Laplace transforms.

 

[PainterGuy]

Thank you for your help!

Your ODE is nonlinear in the unknown $y$.

Is it okay to assume that Laplace transform cannot be used with nonlinear differential equations? The answer given here, https://www.quora.com/Can-you-determine-the-Laplace-Transform-of-a-non-linear-differential-equation , agrees to some extent.

In this case, the substitution $u = y^{1/2}$ will reduce the ODE to one which can be solved by Laplace transforms.

I'm not sure if I'm following you correctly.

The equation reduces to

The new equation is still nonlinear and I can't see a way to apply Laplace transform to it.

I understand that what I wrote above is wrong because "dx" should be represented in term of "dy"; something like this du²/dy. I don't know how to proceed with it. Could you please guide me? Thank you!

 

[Mark44]

Thank you for your help!
Is it okay to assume that Laplace transform cannot be used with nonlinear differential equations? The answer given here, https://www.quora.com/Can-you-determine-the-Laplace-Transform-of-a-non-linear-differential-equation , agrees to some extent.
I'm not sure if I'm following you correctly.

View attachment 246135

The equation reduces to

View attachment 246136

The new equation is still nonlinear and I can't see a way to apply Laplace transform to it.

I understand that what I wrote above is wrong because "dx" should be represented in term of "dy"; something like this du²/dy. I don't know how to proceed with it. Could you please guide me? Thank you!

But $\frac{du^2}{dx} = \frac{du^2}{du}\frac{du}{dx} = 2u\frac{du}{dx}$ using the chain rule. This leads to a very simple, linear DE that you can use Laplace transforms on if you must, but much simpler techniques can be used.

 

[PainterGuy]

Thank you!

I was able to solve it. So, I'd say that saying that a nonlinear differential equation cannot be solved using Laplace transform is not a correct statement.

Note to self:
"y" is expressed in terms of "u", or as a function of "u". "u" in turn being function of "x". "y" is still a function of "x" but to make things easier we introduced substitution variable, u, and it stands between "y" and "x"; in other words, "y" depends upon "u" and "u" depends upon "x".

y=u^2
dy/dx=dy/du * du/dx
dy/dx=du^2/du * du/dx