Solving a Multifluid Manometer Problem to Find P1

[fishingspree2]

Homework Statement

Hello
This is not a homework, but an example in my textbook that I don't really understand.

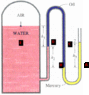
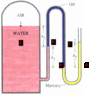
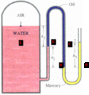
We need to find P₁
The website I took this picture from explains it but it looks too complicated. The teacher did it moving along the tube and it looked really easy but I didn't understand. He almost did it in his head without using the board.

Homework Equations

p_bottom = p_top +ρgh
the pressure at two points that have the same height are the same if they are connected with the same fluid.

The Attempt at a Solution

Find P₁
Here's my try:

P_E=P_air+ρ_watergh₁
P_E=P_D
I don't know how to continue
I know I need to relate P_D to the other known quantities but I don't really see how.

Another question: Isn't P₁ = P_air ? Since 1 is at the boundary of air and water

Thank you for your help

 

[Borek]

No idea what P₁ is.

I guess D means the point where the water and oil meet, B & C look well defined as well, but what are A & E?

 

[fishingspree2]

P₁ is the point where air and water meet.

the answer, if it helps, is:

P₁ = P_atm - ρ_watergh₁ - ρ_oilgh₂ + ρ_mercurygh₃

 

[Borek]

Go from the outside - if you know pressure at C (P_atm), can you calculate pressure at B?