- #1
Rain10399
- 13
- 2
Homework Statement
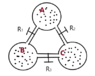
An adiabatic isolated system is formed of three identical balloons (of unknown volume). The balloons are joined by tubes of negligible volume. Each tube has a faucet/tap that is initially closed. The balloons have different quantities of the same ideal gas.
After opening only faucet R1, the system including balloons B and A reaches a state of equilibrium that has pressure p1 and temperature T1.
After opening only faucet R2, the system including balloons A and C reaches a state of equilibrium that has pressure p2 and temperature T2.
After opening only faucet R3, the system including balloons C and B reaches a state of equilibrium that has pressure p3 and temperature T3.
Find the initial pressure of the gas in each balloon (pA, pB and pC).
The drawing:
Also, the book that I'm using has the following results at the end:
pA=p2+p3-p1
pB=p3+p1-p2
pC=p1+p2-p3
Homework Equations
PV=nRT
PVγ = constant (adiabatic process)
The Attempt at a Solution
I tried to apply PV=nRT, but nothing that I did so far worked. I will edit the post if I have any ideas.